Historically, the Rummikub game was played with two sets of cards. Because this required quite some space on the table, modern versions of the game replaced cards by 106 smaller tiles: two sets of tiles that range in value from one to thirteen, in four colors (red, yellow, blue and black), and two joker tiles ($$2 \times 13 \times 4 + 2 = 106$$).

At the start of the game, the pool of tiles is shuffled together and spread out face down across the table so that the face of the tiles is not revealed to the players. Each player draws and reveals one tile. The player whose tile has the highest number value will start the game. Tiles are returned to the pool, and players in turn collect 14 random tiles and arrange them on their racks. Play then begins with the starting player, and proceeds in a clockwise direction.

In the Rummikub game, players each have a rack (container) to store tiles, without revealing the face of the tiles to the other players.

For a player's first move, he must play a set with a value of at least 30 points. Point values are taken from the face value of each tile played, with the joker (if played) assuming the value of the tile it is being used in place of. The player may not use other players' tiles to make the initial 30 or more. A player's first move is known as the initial meld. If a player cannot make an initial meld, he must pick up a single tile from the pool and add it to his rack. Play then proceeds to the next player. Game play continues until a player has used all of the tiles in the rack, at which point he should call out "Rummikub" and is declared the winner.

Assignment

A tile in the Rummikub game is represented as a string (str) that starts with an integer from the range $$[1, 13]$$ that represents the value of the tile, followed by a single uppercase letter that represents its color: R (red), Y (yellow), B (blue) or K (black). We don't take jokers into account.

A collection of tiles that is played on the table is represented as a list, a tuple or a set of tiles. According to the rules of the game, a collection of tiles can only be played if it contains at least three tiles and if all tiles are different. Apart from these two basic conditions, the rules of the game make a distinction between two valid types of collections that can be played on the table: groups and runs.

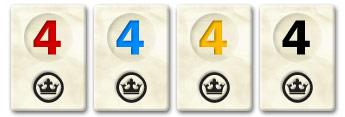
A group of tiles is a collection of tiles that all have the same value but a distinct color. Below, you see an example of a group of four tiles: 4 red, 4 blue, 4 yellow and 4 black.

A group of four tiles: 4 red, 4 blue, 4 yellow and 4 black.

A run of tiles is a collection of tiles that all have the same color and that can be arranged in such a way that the values form a sequence of consecutive integers. The value 1 does not follow the value 13. Below, you see an example of a run of five tiles: 6 blue, 7 blue, 8 blue, 9 blue and 10 blue.

A run of five tiles: 6 blue, 7 blue, 8 blue, 9 blue and 10 blue.

Your task:

Write a function group that takes a list, a tuple or a set of tiles. The function must return a Boolean value (bool) that indicates whether the given tiles are a valid group of tiles.
Write a function run that takes a list, a tuple or a set of tiles. The function must return a Boolean value (bool) that indicates whether the given tiles are a valid run of tiles.

Example

>>> group(['4R', '4B', '4Y', '4K'])
True
>>> group({'6B', '7B', '8B', '9B', '10B'})
False
>>> group(('11R', '2B', '7Y', '2B', '9K'))
False

>>> run(['4R', '4B', '4Y', '4K'])
False
>>> run({'6B', '7B', '8B', '9B', '10B'})
True
>>> run(('11R', '2B', '7Y', '2B', '9K'))
False