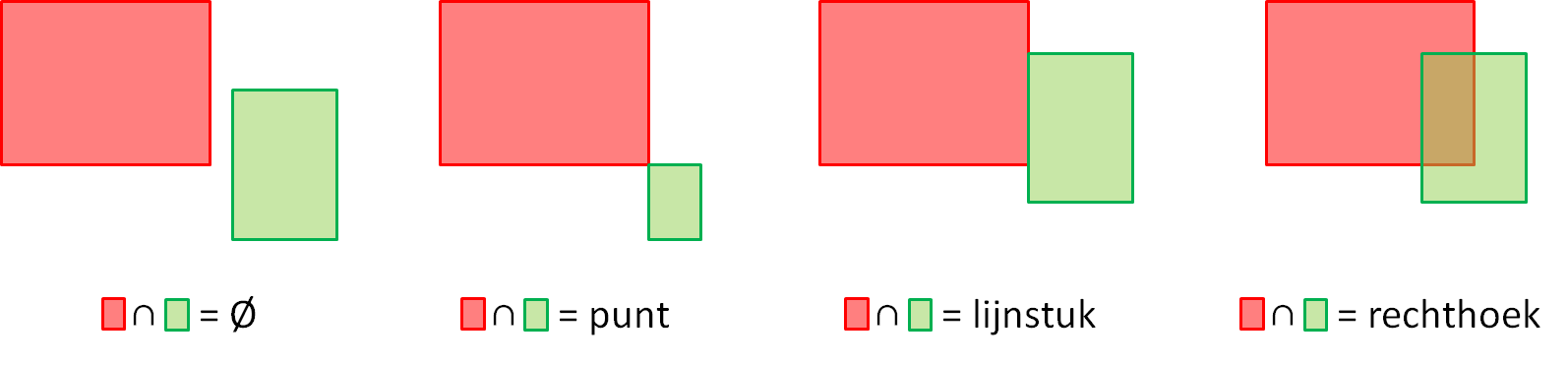
If we want to determine the intersection of two given rectangles in the Euclidean surface, there are four possibilities. The intersection is either empty, a point (common vertices), a line segment or a rectangle.

Assignment

Define a class Point with which points in the Euclidean surface with whole co-ordinates can be represented. This class must support the following methods:

• An initializing method __init__ that allows to make a point in the Euclidean surface based on a $$x$$ and $$y$$ co-ordinates. Both co-ordinates can be given to the method as the optional parameters x and y ($$x, y \in \mathbb{Z}$$), and have a value zero if they weren't given. The initializing method must appoint the given values or their standard values to the attributes x and y of the newly made object.

• Methods __str__ and __repr__ that both print a string representation of a point given in the format "Point(x, y)", where x and y respectively represent the $$x$$ and $$y$$ co-ordinate of the point in the Euclidean surface. 

• Methods __lt__, __le__, __eq__, __ne__, __gt__ and __ge__ that allow to compare two points from the Euclidean surface using the Python operators <, <=, ==, !=, > and >=. The comparison of two points happens by first comparing their $$x$$ co-ordinates, and then the $$y$$ co-ordinates if the $$x$$ co-ordinates are equal.

• A method distance that can be used to calculate the Euclidean distance between two points in the Euclidean surface. The Euclidean distance between two points $$(x_1, y_1)$$ and $$(x_2, y_2)$$ is given by \[ \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \]

Define a class Linesegment that can be used to represent the line segments in the Euclidean surface that have a length larger than zero. This class must support the following methods: 

• An initializing method __init__ that allows to make a line segment in the Euclidean surface based on two given points. Two object of the class Point must be given to this method, that represent both ends of the line segment. The smallest of these points must be appointed to the attribute point1 of the newly made object by the initializing method, and the largest point to the attribute point2. Watch the example below to verify which action the initializing method should take if the given line segment has length zero.

• Methods __str__ and __repr__ that both print a string representation of the format "Linesegment(Point(x1, y1), Point(x2, y2))", where x1 and y1 respectively represent the $$x$$ and $$y$$ co-ordinate of the smallest endpoint of the line segment and x2 and y2 respectively represent the $$x$$ and $$y$$ co-ordinate of the largest endpoint of the line segment. 

• A method length that can be used to determine the length of a line segment. The length of a line segment is calculated as the Euclidean distance between both endpoints of the line segment.

Definie a class Rectangle with which rectangles can be represented in the Euclidean surface that have an area that is larger than zero. This class must support the following methods: 

• An initializing method __init__ that allows to make a rectangle in the Euclidean surface based on two given vertices that are diametrically situated opposite each other. Two objects of the class Point must be given to this method, that represent the vertices that are diametrically opposite each other in the rectangle. The initializing method must appoint the attributes point1 and point2 of the newly made objects respectively the vertex in the left bottom corner and in the right upper corner. Watch the example below to verify which action the method should take if the given rectangle has an area of zero.

• Methods __str__ and __repr__ that both print the rectangle of the format "Rectangle(Point(x1, y1), Point(x2, y2))", where x1 and y1 respectively represent the $$x$$ and $$y$$ co-ordinate of a vertex in the left bottom corner of the rectangle and x2 and y2 respectively represent the $$x$$ and $$y$$ co-ordinates the vertex in the right upper corner of the rectangle.

• A method area that can be used to determine the area of the rectangle. The area of the rectangle is calculated as the product of the width of the rectangle.

• A method intersection that can be used to determine the intersection of two rectangles This method must print the value None if the rectangles don't intersect, or an object of the classes Point, Linesegment or Rectangle that describes the overlap of the two rectangle as a common vertex, a common side or a common rectangle.

Example

>>> p1 = Point(1, 2)
>>> p1
Point(1, 2)
>>> print(p1.x, p1.y)
1 2
>>> p2 = Point(3, 5)
>>> print(p2)
Point(3, 5)
>>> p1 < p2
True
>>> p1.distance(p2)
3.605551275463989

>>> l1 = Linesegment(Point(1,2), Point(3, 4))
>>> l1
Linesegment(Point(1, 2), Point(3, 4))
>>> print(l1.point1, l1.point2)
Point(1, 2) Point(3, 4)
>>> l1.length()
2.8284271247461903
>>> l2 = Linesegment(Point(5, -4), Point(-2, 3))
>>> print(l2)
Linesegment(Point(-2, 3), Point(5, -4))
>>> l2.length()
9.899494936611665
>>> l3 = Linesegment(Point(1,2), Point(1, 2))
Traceback (most recent call last):
AssertionError: line segment must have length larger than zero

>>> r1 = Rectangle(Point(1, 1), Point(4, 4))
>>> r1
Rectangle(Point(1, 1), Point(4, 4))
>>> r1.area()
9
>>> r2 = Rectangle(Point(6, 3), Point(3, 6))
>>> r3 = Rectangle(Point(6, 3), Point(4, 2))
>>> print(r3)
Rectangle(Point(4, 2), Point(6, 3))
>>> r3.area()
2
>>> r4 = Rectangle(Point(-7, -3), Point(1, 1))
>>> r1.intersection(r2)
Rectangle(Point(3, 3), Point(4, 4))
>>> r1.intersection(r3)
Linesegment(Point(4, 2), Point(4, 3))
>>> r2.intersection(r3)
Linesegment(Point(4, 3), Point(6, 3))
>>> r1.intersection(r4)
Point(1, 1)
>>> r5 = Rectangle(Point(1, 1), Point(1, 1))
Traceback (most recent call last):
AssertionError: rectangle must have area larger than zero