Some positive integers are arranged in a triangle, as shown in the figure below.

Construct a path, starting in the topmost node of the triangle, that finds its way to the base of the triangle, level per level, using adjacent numbers, for which the sum of the numbers on the path is as high as possible.

In other words, given this directed graph, find a path from root to a leaf where the sum of the nodes on the path is as high as possible. The solution is given in red in the figure below.

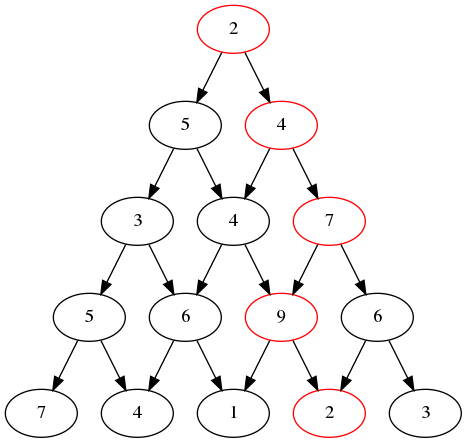
Design and implement an algorithm using dynamic programming for this problem.

Assignment

Write a Python function maximum_descent(triangle:list) that takes as argument a triangular matrix and returns an optimal path, as described above using dynamic programming. The triangle only contains positive integers.

Examples

>>> maximum_descent([[2], [5, 4], [3, 4, 7], [5, 6, 9, 6], [7, 4, 1, 2, 3]])
24
>>> maximum_descent([[13], [1, 8]])
21
>>> maximum_descent([])
0
>>> maximum_descent([[15], [12, 9], [15, 11, 6]])
42
>>> maximum_descent([[4], [9, 4], [3, 8, 4], [9, 3, 2, 10]])
25
>>> maximum_descent([[15], [3, 11], [13, 10, 6], [15, 14, 8, 1], [0, 2, 12, 0, 15]])
62
>>> maximum_descent([[10], [7, 10], [2, 6, 7], [7, 4, 14, 2], [2, 10, 15, 3, 9], [9, 3, 10, 6, 9, 14]])
66