Mathemagician Bob Hummer invented a card curiosity that consists of the following actions:
-
randomly select 10 cards from an ordinary deck and hold this packet face down in your left hand
-
remove the top two cards from the packet, turn them around and put them back on top of the packet
-
cut the packet anywhere you like; in cutting a packet the packet is split in two packets and the top packet is moved to the bottom of the other packet
-
repeat steps (2) and (3) for as long as you like, turning over the top two cards and cutting the packet
-
when you've finished step (4), deal the cards in a row on the table and turn over the cards at even positions in the row: the second, fourth, sixth, eighth and tenth cards
This will always leave five cards face up.
The schematic below shows a detailed example of the card trick, in which the positions of the cards in the packet are numbered top to bottom from 1 to 10. Each card is represented with a unique color and the bulge indicates whether the card is turned face up or face down. Steps (2) and (3) are repeated three times in this example, in which we successively cut after 4, 5 and 3 cards in step (3) of the card trick. Finally, after step (5) the second, third, sixth, eighth and ninth card face up.
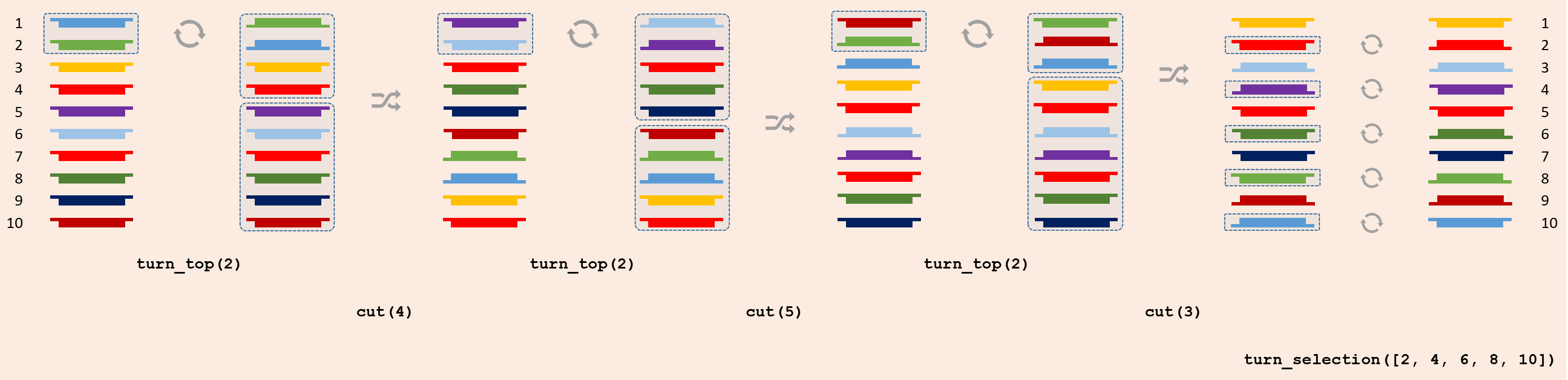
Afterwards Persi Daconis and Ron Graham proved that this trick works in general for any packet of $$2n$$ cards, leaving $$n$$ cards facing up after step (5).
Assignment
A standard card deck includes 52 different cards, evenly distributed over four suits: 13 clubs (♣), 13 diamonds (♦), 13 hearts (♥) and 13 spades (♠). Clubs and spades are black, whereas diamonds and hearts are red. Each suit includes thirtheen ranks: two through ten (with each card depicting that many symbols of the suit), jack, queen, king (each depicted with a symbol of its suit) and ace (depicting a single symbol of its suit). Commercial card decks may also include anywhere from one to six jokers, but we do not take these into account here.
Each card of a standard 52-card deck is represented by a string that contains the rank of the card, followed by its suit:
-
ranks: 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), K (king) and A (ace)
-
suits: C (clubs; ♣), D (diamonds; ♦), H (hearts; ♥) and S (spades; ♠)
As such, the ace of spades is for example represented as AS, the ten of hearts as 10H and the king of clubs as KC. In addition we use uppercase for face-up cards (e.g. AS or 10H) and lowercase for face-down cards (e.g. as or 10h). Note that the last character of the string representation of a card is always an uppercase or lowercase letter (not a digit) that indicates the suit of the card.
The list representation of a packet of cards consists of a list (list) containing the string representations of the consecutive cards in the packet, where the first element of the list is the top card in the packet. Some cards of the packet are facing up, where the other are facing down. A packet of cards does not necessarily need to contain all 52 cards of a standard deck, but a card may not occur more then once in the packet.
Your task:
-
Write a function is_valid_card that takes a single argument. The function must return a Boolean value that indicates whether the given argument is a valid string representation of a card.
-
Write a function string_representation that takes the list representation of a packet containing $$n \in \mathbb{N}_0$$ cards. The function must return a string representation (str) of the packet that consist of the representations of the consecutive cards in the packet (top to bottom), each time separated by a single space. Cards facing up are represented in their default string representation. Cards facing down as represented as a double asterisk (**).
-
Write a function turn_selection that takes the list representation of a packet containing $$n \in \mathbb{N}_0$$ cards. As an optional second argument a sequence (list of tuple) of positions in the packet can also be passed, with card positions numbered top to bottom from 1 to $$n$$. The function may assume that all given positions are valid and that each position occurs at most once. The function must individually turn all cards at the given positions, with none of the cards changing position in the packet. If no second argument is passed to the function then all cards must be turned individually, with the none of the cards changing position in the packet.
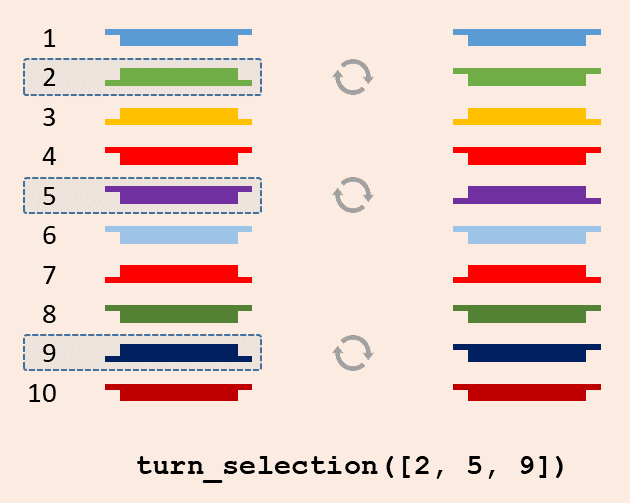
Individually turn the second, fifth and ninth card, without changing their position in the packet. -
Write a function turn_top that takes two arguments: i) the list representation of a packet containing $$n \in \mathbb{N}_0$$ cards and ii) a number of cards $$a \in \mathbb{N}$$ ($$0 \leq a \leq n$$). The function must remove the top $$a$$ cards from the packet, turn them around as a whole and put them back on top of the packet. This is the action that is executed in step (2) of the card trick with $$a = 2$$.
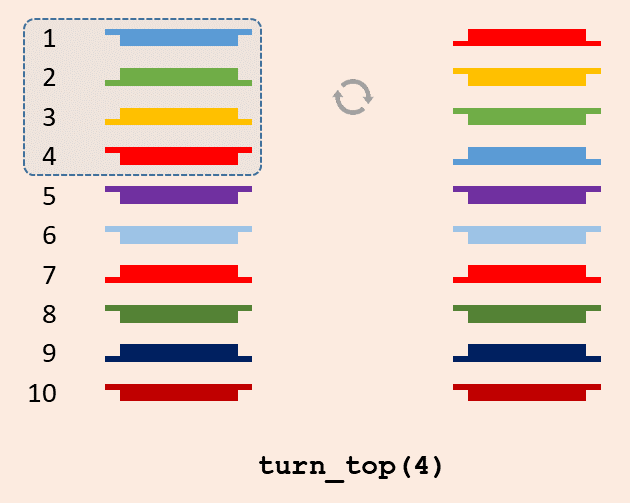
Turn the top four cards of the packet. -
Write a function cut that takes two arguments: i) the list representation of a packet containing $$n \in \mathbb{N}_0$$ cards and ii) a number of cards $$a \in \mathbb{N}$$ ($$0 \leq a \leq n$$). The function must move the top $$a$$ cards to the bottom of the remaining cards of the packet. This is the action that is executed in step (3) of the card trick.
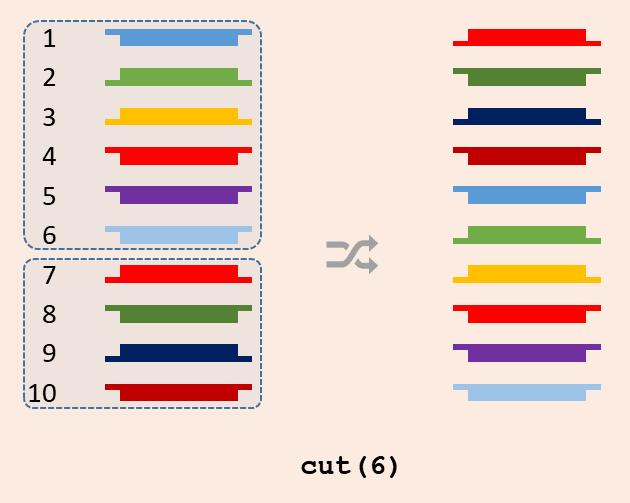
Cut the deck after six cards.
The functions string_representation, turn_selection, turn_top and cut all take the list representation of a packet containing $$n \in \mathbb{N}_0$$ cards as their first argument. If this argument does not represent a valid list representation, an AssertionError must be raised with the message invalid packet.
All functions turn_selection, turn_top en cut must modify the given list representation of the packet of cards and return a reference to this packet. The function string_representation may not modify the given list representation of the packet of cards.
Example
The following interactive session simulates the successive actions that we gave in the introduction as an example of the card trick (see figure).
>>> is_valid_card('AS')
True
>>> is_valid_card('10h')
True
>>> is_valid_card('KC')
True
>>> is_valid_card(42)
False
>>> is_valid_card('11d')
False
>>> is_valid_card('7X')
False
>>> is_valid_card('qC')
False
>>> stack = ['AH', '3S', 'KC', '4H', '3D', '10H', '8D', '5D', '7C', 'QS']
>>> string_representation(stack)
'AH 3S KC 4H 3D 10H 8D 5D 7C QS'
>>> turn_selection(stack)
['ah', '3s', 'kc', '4h', '3d', '10h', '8d', '5d', '7c', 'qs']
>>> string_representation(stack)
'** ** ** ** ** ** ** ** ** **'
>>> turn_top(stack, 2)
['3S', 'AH', 'kc', '4h', '3d', '10h', '8d', '5d', '7c', 'qs']
>>> string_representation(stack)
'3S AH ** ** ** ** ** ** ** **'
>>> cut(stack, 4)
['3d', '10h', '8d', '5d', '7c', 'qs', '3S', 'AH', 'kc', '4h']
>>> string_representation(stack)
'** ** ** ** ** ** 3S AH ** **'
>>> turn_top(stack, 2)
['10H', '3D', '8d', '5d', '7c', 'qs', '3S', 'AH', 'kc', '4h']
>>> string_representation(stack)
'10H 3D ** ** ** ** 3S AH ** **'
>>> cut(stack, 5)
['qs', '3S', 'AH', 'kc', '4h', '10H', '3D', '8d', '5d', '7c']
>>> string_representation(stack)
'** 3S AH ** ** 10H 3D ** ** **'
>>> turn_top(stack, 2)
['3s', 'QS', 'AH', 'kc', '4h', '10H', '3D', '8d', '5d', '7c']
>>> string_representation(stack)
'** QS AH ** ** 10H 3D ** ** **'
>>> cut(stack, 3)
['kc', '4h', '10H', '3D', '8d', '5d', '7c', '3s', 'QS', 'AH']
>>> string_representation(stack)
'** ** 10H 3D ** ** ** ** QS AH'
>>> turn_selection(stack, [2, 4, 6, 8, 10])
['kc', '4H', '10H', '3d', '8d', '5D', '7c', '3S', 'QS', 'ah']
>>> string_representation(stack)
'** 4H 10H ** ** 5D ** 3S QS **'
>>> stack = ['AH', '3S', 'KC', '4H', '3D', '11H', '8D', '5D', '7C', 'QS']
>>> string_representation(stack)
Traceback (most recent call last):
AssertionError: invalid stack
>>> turn_selection(stack)
Traceback (most recent call last):
AssertionError: invalid stack
>>> turn_top(stack, 2)
Traceback (most recent call last):
AssertionError: invalid stack
>>> cut(stack, 2)
Traceback (most recent call last):
AssertionError: invalid stack