In the contentious presidential election of 1876, the campaign of Democrat Samuel Tilden sent many enciphered messages to its agents in contested states.

The United States presidential election of 1876 was the 23rd quadrennial presidential election, held on Tuesday, November 7, 1876. It was one of the most contentious and controversial presidential elections in American history. The results of the election remain among the most disputed ever, although it is not disputed that Samuel J. Tilden (left) of New York outpolled Ohio's Rutherford B. Hayes (right) in the popular vote. After a first count of votes, Tilden won 184 electoral votes to Hayes's 165, with 20 votes unresolved. These 20 electoral votes were in dispute in four states. In the case of Florida, Louisiana, and South Carolina, each party reported its candidate had won the state, while in Oregon one elector was replaced after being declared illegal for being an "elected or appointed official". The question of who should have been awarded these electoral votes is the source of the continued controversy concerning the results of this election.

Two years after the election, the New York Daily Tribune published some of the deciphered telegrams, showing that Tilden's campaign had tried to bribe election officials to win the race. Here's one of the telegrams:

Enciphered telegram sent by Samuel Tilden's campaign team.

Since only 10 letters are used, it seems likely that the cipher refers to pairs of letters (bigrams). So if each successive pair in the message is assigned to an arbitrary letter

Mapping of successive letter pairs onto different letters of the alphabet.

then we have a simple cryptogram that can be solved to give the message:

Deciphered version of the telegram that was sent by Samuel Tilden's campaign team.

Tilden's campaign did the same thing with pairs of numbers. For example, this message

Enciphered telegram sent by Samuel Tilden's campaign team.

turns out to mean:

Deciphered version of the telegram that was sent by Samuel Tilden's campaign team.

In 1879 the Tribune's experts worked out the letter and number pairs that had corresponded to each letter of the alphabet:

Complete bigram mapping of letters and numbers onto the different letters of the alphabet.

But it wasn't until 1952 that cryptographer William F. Friedman reconstructed the table the agents had used to remember the encryption key:

It wasn't until 1952 that cryptographer William F. Friedman reconstructed the table that the agents had used to remember the encryption key.

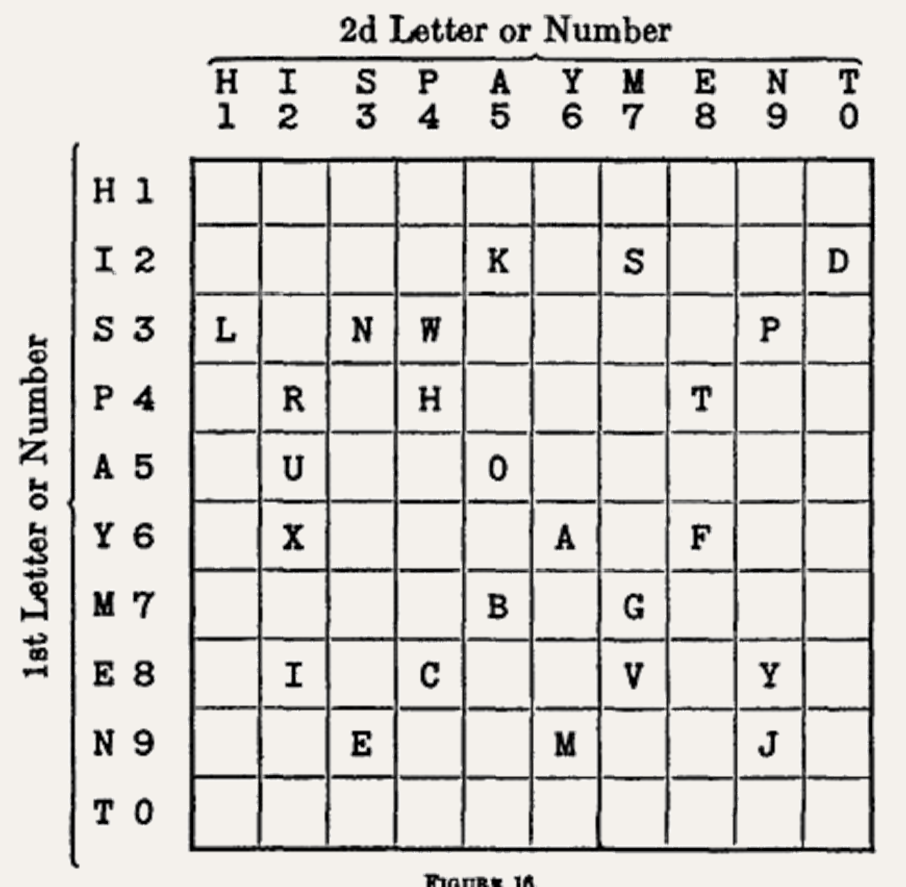
Beaird Glover wrote in his 1991 book Secret Ciphers of the 1876 Presidential Election:

"It is amusing to note that the conspirators selected as their key a phrase quite in keeping with their attempted illegalities — HIS PAYMENT — for bribery seems to have played a considerable part in that campaign."

Assignment

Encode en decode messages using the ciphers that have been used by Samual Tilden's campaign team. Encoding is done by replacing all letters in a message by bigrams composed of two uppercase letters. In encoding a message, no distinction is made between uppercase and lowercase letters, and all characters that are no letters of the alphabet are ignored.

A cipher key is composed of two components. The first component is a keyword containing different uppercase letters that are used to label the rows and columns of a square grid. In the following example, we have used the keyword ABCD to label the rows (from top to bottom) and columns (from left to right).

Example of a table used to encode and decode messages.

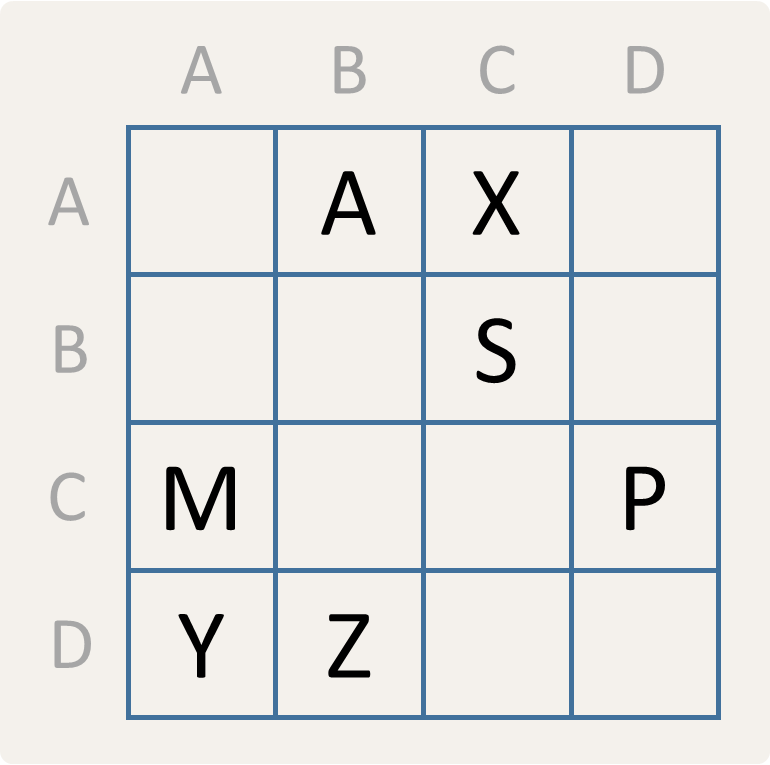
The second component is a description that indicates how a number of different letters of the alphabet have to be arranged in the square grid. Such a description alternates between sequences of successive capitals and natural numbers (that may contain multiple digits), and can start either with a capital or a natural number. The description is used to fill the square grid with the capitals included in the description. This is done by starting at the cell in the upper left corner. A capital indicates that the letter must be entered into the current cell. A natural number indicates that the corresponding number of cells must be skipped if we traverse the cells from left to right and from top to bottom. As such, the arrangement of letters in the sample grid above corresponds to the description 1AX3S1M2PYZ. Note that after the final Z in the description we could have added another number 2 to indicate that the last two cells of the grid are empty, but this is optional.

Define a class Cipher to represent ciphers that can encode and decode messages. The operation of the cipher is fixed by passing a keyword (str) and a description (str) when creating a new cipher (Cipher). The class may assume that only valid keywords and descriptions are passed, without the need to check this explicitly. A cipher $$c$$ (Cipher) is immutable and must at least have the following properties:

A property grid that represents the square grid used by cipher $$c$$. This grid is represented as a list containing the rows of the grid (from top to bottom), where each row is itself represented as a list of characters (str; from left to right). The elements of each row are the capitals found in the corresponding cells of the grid, or a dash (-) in case the cell does not contain a capital.
A property map that refers to a dictionary (dict) that maps each letter (str) from the grid used by cipher $$c$$ onto the bigram (str) that is composed of the two letters used to respectively label the row and column where the letter is found in the grid.

In addition, the cipher $$c$$ (Cipher) must support at least the following methods:

A method encode that takes a message (str). The method must return the encoded message (str; in uppercase) obtained when applying cipher $$c$$. In encoding, only the letters in the given message are taken into account (all characters that are not letters are simply ignored), and no distinction is made between uppercase and lowercase letters. In case the given message cannot be encoded with cipher $$c$$, an AssertionError must be raised with the message invalid message.
A method decode that takes a message (str) that was encoded with cipher $$c$$ (cfr. method encode). The method must return the letters (str; in uppercase) in the original message. If the given message cannot be decoded with cipher $$c$$, an AssertionError must be raised with the message invalid message.

Example

        >>> cipher = Cipher('ABCD', '1AX3S1M2PYZ')
>>> cipher.grid
[['-', 'A', 'X', '-'], ['-', '-', 'S', '-'], ['M', '-', '-', 'P'], ['Y', 'Z', '-', '-']]
>>> cipher.map
{'A': 'AB', 'X': 'AC', 'S': 'BC', 'M': 'CA', 'P': 'CD', 'Y': 'DA', 'Z': 'DB'}
>>> cipher.encode('spam')
'BCCDABCA'
>>> cipher.decode('BCCDABCA')
'SPAM'
>>> cipher.encode('eggs')
Traceback (most recent call last):
AssertionError: invalid message
>>> cipher.decode('BCCDBACA')
Traceback (most recent call last):
AssertionError: invalid message

>>> cipher02 = Cipher('HISPAYMENT', '14K1S2DL1NW4P2R1H3T3U2O6X3A1F6B1G4I1C2V1Y3E2M2J')
>>> cipher02.grid
[['-', '-', '-', '-', '-', '-', '-', '-', '-', '-'], ['-', '-', '-', '-', 'K', '-', 'S', '-', '-', 'D'], ['L', '-', 'N', 'W', '-', '-', '-', '-', 'P', '-'], ['-', 'R', '-', 'H', '-', '-', '-', 'T', '-', '-'], ['-', 'U', '-', '-', 'O', '-', '-', '-', '-', '-'], ['-', 'X', '-', '-', '-', 'A', '-', 'F', '-', '-'], ['-', '-', '-', '-', 'B', '-', 'G', '-', '-', '-'], ['-', 'I', '-', 'C', '-', '-', 'V', '-', 'Y', '-'], ['-', '-', 'E', '-', '-', 'M', '-', '-', 'J', '-'], ['-', '-', '-', '-', '-', '-', '-', '-', '-', '-']]
>>> cipher02.map
{'K': 'IA', 'S': 'IM', 'D': 'IT', 'L': 'SH', 'N': 'SS', 'W': 'SP', 'P': 'SN', 'R': 'PI', 'H': 'PP', 'T': 'PE', 'U': 'AI', 'O': 'AA', 'X': 'YI', 'A': 'YY', 'F': 'YE', 'B': 'MA', 'G': 'MM', 'I': 'EI', 'C': 'EP', 'V': 'EM', 'Y': 'EN', 'E': 'NS', 'M': 'NY', 'J': 'NN'}
>>> cipher02.encode('Have Marble and Coyle telegraph for influential men from Delaware and Virginia.')
'PPYYEMNSNYYYPIMASHNSYYSSITEPAAENSHNSPENSSHNSMMPIYYSNPPYEAAPIEISSYESHAINSSSPEEIYYSHNYNSSSYEPIAANYITNSSHYYSPYYPINSYYSSITEMEIPIMMEISSEIYY'
>>> cipher02.decode('PPYYEMNSNYYYPIMASHNSYYSSITEPAAENSHNSPENSSHNSMMPIYYSNPPYEAAPIEISSYESHAINSSSPEEIYYSHNYNSSSYEPIAANYITNSSHYYSPYYPINSYYSSITEMEIPIMMEISSEIYY')
'HAVEMARBLEANDCOYLETELEGRAPHFORINFLUENTIALMENFROMDELAWAREANDVIRGINIA'
>>> cipher02.encode('Indications of weakening here.')
'EISSITEIEPYYPEEIAASSIMAAYESPNSYYIANSSSEISSMMPPNSPINS'
>>> cipher02.decode('EISSITEIEPYYPEEIAASSIMAAYESPNSYYIANSSSEISSMMPPNSPINS')
'INDICATIONSOFWEAKENINGHERE'
>>> cipher02.encode('Press advantage and watch Board.')
'SNPINSIMIMYYITEMYYSSPEYYMMNSYYSSITSPYYPEEPPPMAAAYYPIIT'
>>> cipher02.decode('SNPINSIMIMYYITEMYYSSPEYYMMNSYYSSITSPYYPEEPPPMAAAYYPIIT')
'PRESSADVANTAGEANDWATCHBOARD'