The Collatz conjecture is a conjecture from number theory. It
is based on a sequence of numbers — referred to as the hailstone
sequence — that is constructed in the following way: take any
integer $$n$$. If $$n$$ is even, divide it by 2 to get $$n / 2$$. If $$n$$
is odd, multiply it by 3 and add 1 to obtain $$3n + 1$$. The Collatz
conjecture states that no matter what integer $$n$$ ($$n \geq 1$$) you
start with, you will eventually always reach 1. This conjecture has been
first proposed by Lothar Collatz in 1937. Up until now this conjecture has
neither been proven nor rejected.
As an example, let's start from the number $$n = 12$$. The hailstone
sequence that results from this number reads as follows:
12, 6, 3, 10, 5, 16, 8, 4, 2, 1
Based on this sequence it is said that the cycle length for $$n = 12$$ is equal to 10, because the length of the corresponding hailstone sequence (including the last value 1) is equal to 10. If we start from the number $$n = 15$$, we have a much longer hailstone sequence with cycle length 18:
15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
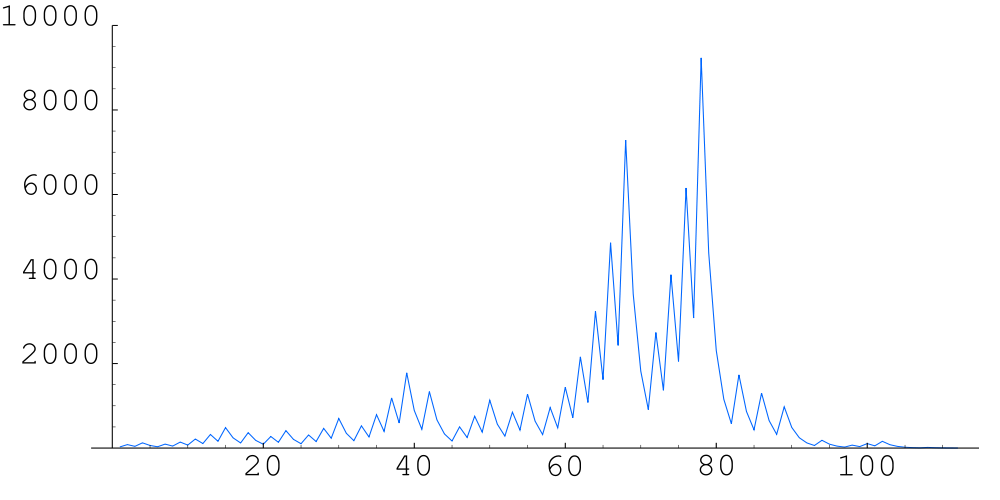
For $$n = 27$$ the cycle length is as high as 112, climbing up to a maximal value above 9000 before descending to 1:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
The figure below illustrates the evolution of the hailstone sequence for $$n = 27$$.
Input
The input contains $$t$$ test cases ($$t \leq 100$$). The first line of the input contains the integer $$t$$. It is followed by $$t$$ lines that each contain an integer $$n$$ ($$n \geq 1$$).
Output
For each test case, print the cycle length for $$n$$ on a separate line.
Example
Input:
5
1
2
321
1111111111111
111111111111111111111111111111111111111111111111111111111111Output:
1
2
25
261
1296Epilogue
What's the use of the Collatz conjecture? The figure below shows a possible use case.