For thousands of years, cities have been the manifestation of humankind's artistry, imagination, and instinct to succeed. They embody our strong social desires and longing to create grand masterpieces. London, Constantinople, Paris, New York, Ancient Rome and Tokyo have been just a few of the dazzling trophies mankind has built. But there have been many cases in which someone's vision for a better, more efficient, or more fantastic city collapsed into a heap of broken dreams.

Buckminster Fuller¹ was a brilliant visionary, architect, scientist, environmentalist and philosopher who, in the 1960s, developed a bold design for a floating utopia that was dubbed Triton City. It would have been assembled from tetrahedral² modules, starting with a floating neighborhood of 5000 residents, with an elementary school, a supermarket and a few specialty shops. Three to six neighborhoods would form a town, and three to seven towns would form a city. At each stage the corresponding infrastructure would be added: schools, civic facilities, government offices, and industry. A full-sized city might accommodate 100.000 people in a single building.

Fuller was initially commissioned by a wealthy Japanese patron to design a floating city for Tokyo Bay. He died in 1966, but astoundingly enough, the United States Department of Urban Development³ (HUD) commissioned Fuller for further design and analysis. His designs called for the city to be resistant to tsunamis, provide the most possible outside living, desalinate the very water that it would float in for consumption, give privacy to each residence, and incorporate a tetrahedronal shape which provides the most surface area with the least amount of volume. Everything from education to entertainment to recreation would be a part of the city. Fuller also claimed that the low operating costs would result in a high standard of living. This is part of the document that Fuller wrote to convince the government about his ideas:

In the early 1960s I was commissioned by a Japanese patron to design one of my tetrahedronal floating cities for Tokyo Bay. Three-quarters of our planet Earth is covered with water, most of which may float organic cities. Floating cities pay no rent to landlords. They are situated on the water, which they desalinate and recirculate in many usefuland non-polluting ways. They are ships with all an ocean ship's technical autonomy, but they are also ships that will always be anchored. They don't have to go anywhere. Their shape and its human-life accommodations are not compromised, as must be the shape of the living quarters of ships whose hull shapes are constructed so that they may slip, fishlike, at high speed through the water and high seas with maximum economy. Floating cities are designed with the most buoyantly stable conformation of deep-sea bell-buoys. Their omni-surface-terraced, slop-faced, tetrahedronal structuring is employed to avoid the lethal threat of precipitous falls by humans from vertically sheer high-rising buildings.

HUD eventually sent the plans to the U.S. Navy where they were dissected and analyzed even further. The city of Baltimore, upon hearing of the project, became interested and petitioned to have Triton City moored off of its shores in Chesapeake Bay. However, as municipal and federal administrations changed, the project languished and was never brought to light. Today, there are derivatives of Triton City — such as the artificial island Kansai and its airport in Osaka⁴, Japan — but they pale in comparison to the scope of Triton City.

Assignment

The factorial $$n!$$ of an integer $$n \in \mathbb{N}$$ is computed as the product of all strictly positive integers less than or equal to $$n$$. \[n! = \prod_{k=1}^{n}k = 1 \times 2 \times 3 \times \cdots \times n\] According to the convention for an empty product, the value of $$0! = 1$$. The binomial coefficient $$\binom{n}{k}$$ This is an important statistic used in combinatorics that expresses the number of ways one can choose $$k \in \mathbb{N}$$ elements from a set of $$n \in \mathbb{N}$$ elements. \[\binom{n}{k} = \begin{cases}\frac{n!}{k!(n-k)!} & \mbox{if } 0 \leq k \leq n \\ 0 &  \mbox{if } k \lt 0 \mbox{ or } k \gt n \end{cases}\] The triangular number $$T_n$$ counts the number of circles that can form an equilateral triangle having $$n \in \mathbb{N}$$ circles on each side.

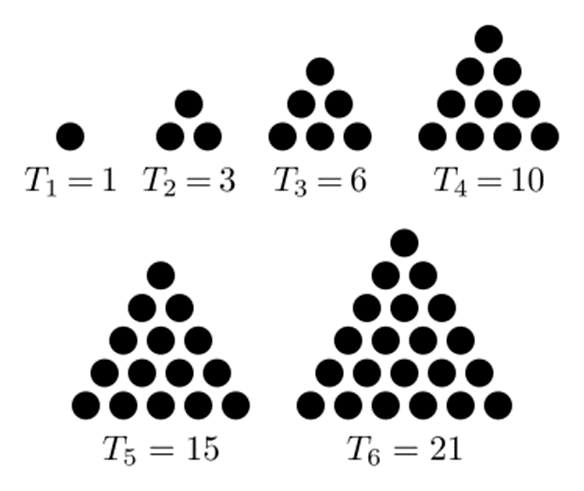
A triangular number is thus equal to the sum of all integers less than or equal to $$n$$. \[T_n = \sum_{k=1}^{n}k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} = \binom{n+1}{2}\] The tetrahedral number $$P_n$$ counts the number of spheres that can form a tetrahedron (a pyramid with a triangular base and three sides) having $$n \in \mathbb{N}$$ spheres on each side.

The $$n$$-th tetahedral number is thus equal to the sum of the first $$n$$ triangular numbers. \[P_n = \sum_{k=1}^{n}T_k = \frac{n(n+1)(n+2)}{6} = \binom{n+2}{3}\] Your task:

• Write a function factorial that takes an integer $$n \in \mathbb{N}$$ (int) and returns $$n!$$ (int).

• Write a function binomial that takes two integers $$n, k \in \mathbb{N}$$ (int), such that $$n \geq k$$. The function must return the binomial coefficient $$\binom{n}{k}$$ (int).

• Write a function triangular that takes an integer $$n \in \mathbb{N}$$ (int) and returns the $$n$$-th triangular number $$T_n$$ (int).

• Write a function tetrahedral that takes an integer $$n \in \mathbb{N}$$ (int) and returns the $$n$$-th tetrahedral number $$P_n$$ (int).

Example

>>> factorial(10)
3628800
>>> factorial(32)
263130836933693530167218012160000000

>>> binomial(7, 3)
35
>>> binomial(12, 4)
495

>>> triangular(10)
55
>>> triangular(32)
528

>>> tetrahedral(10)
220
>>> tetrahedral(32)
5984

Epilogue

The Line⁶ (Arabic: ذا لاين) is a proposed smart linear city Saudi Arabia wants to build in Neom, Tabuk.

The 170-kilometre long city is designed to preserve nature. It will have no cars, streets or carbon emission, but is connected by an underground train that runs on hydrogen. Building the city is a prestige project of Saudi Crown Prince Mohammed bin Salman and is part of the Saudi Vision 2030⁷ project. He hopes The Line will boost the image of his country and gain political, economic and geostrategic advantage. Saudi Arabia claims The Line will create 380,000 jobs and add $48 billion to the country's GDP. The city's plans anticipate a population of 9 million inhabitants and a total estimated cost of $500 billion.