The king of a small country invites 1000 senators to his annual party. As a tradition, each senator brings the king a bottle of wine. Soon after, the queen discovers that one of the senators is trying to assassinate the king by giving him a bottle of poisoned wine. Unfortunately, they do not know which senator, nor which bottle of wine is poisoned, and the poison is completely indiscernible.

However, the king has 10 prisoners he plans to execute. He decides to use them as taste testers to determine which bottle of wine contains the poison. The poison when taken has no effect on the prisoner until exactly 24 hours later when the infected prisoner suddenly dies. The king needs to determine which bottle of wine is poisoned by tomorrow so that the festivities can continue as planned. Hence he only has time for one round of testing. How can the king administer the wine to the prisoners to ensure that 24 hours from now he is guaranteed to have found the poisoned wine bottle?

Here is one possible solution. We have 1000 bottles of wine, one of which is poisoned and somehow we need to test all of the wine bottles using only 10 prisoners as taste testers. However we decide to administer the wine to the prisoners, we need to use the prisoners' deaths as a code to trace back to the poisoned wine bottle.

Since we have only 24 hours to test the wine, we know that there is not enough time nor enough prisoners to test the wine one-by-one. I'm guessing you got to this point and that's where the confusion sets in.

How can we test all of the bottles? Well, we're going to have to get the prisoners drunk, I can tell you that much! Just kidding, but seriously we need to systematically distribute the wine to the prisoners so that there are at least a thousand different combinations. First, let's label the wine bottles 0–999 so we can tell them apart. Also, we line up our 10 prisoners and label them A-J.

We now have prisoner A drink a little from every other bottle, starting with the second bottle (the bottle that has been labeled #1). In other words, prisoner A will drink from bottles #1, #3, #5, …

Next, assign prisoner B the task of drinking from every other set of two bottles. In particular, he skips bottles #0 and #1 and drinks from bottles #2 and #3. Then, again, he skips bottles #4 and #5 and drinks from bottles #6 and #7, and so forth continuing the pattern.

Have prisoner C drink from every other set of four bottles: i.e. prisoner C drinks from bottles #4-7 (skips #0-3), #12-15 (skips #8-11), #20-23, …

Are you seeing the pattern? Keep doubling the number of bottles each prisoner drinks in succession. Prisoner D drinks from every other set of eight bottles, prisoner E from every other set of 16, prisoner F from every other set of 32, prisoner G from every other set of 64, prisoner H from every other set of 128, prisoner I from every other set of 256 and lastly, prisoner J doesn't drink from the first 512 bottles.

At this point, you may notice something looks familiar. The bottle assignments reflect powers of 2.

We have successfully distributed the wine so that there are sufficiently many combinations. Now we wait 24 hours to see which prisoners were poisoned.

But, how will we be able to tell which bottle was the poisonous one? We will look at the pattern of poisoned prisoners encoded in binary. To do so we will place a one above the prisoners who are poisoned, and a zero above those who aren't. Before we decode the result, we need to flip our prisoners around so that it matches the binary place-value system.

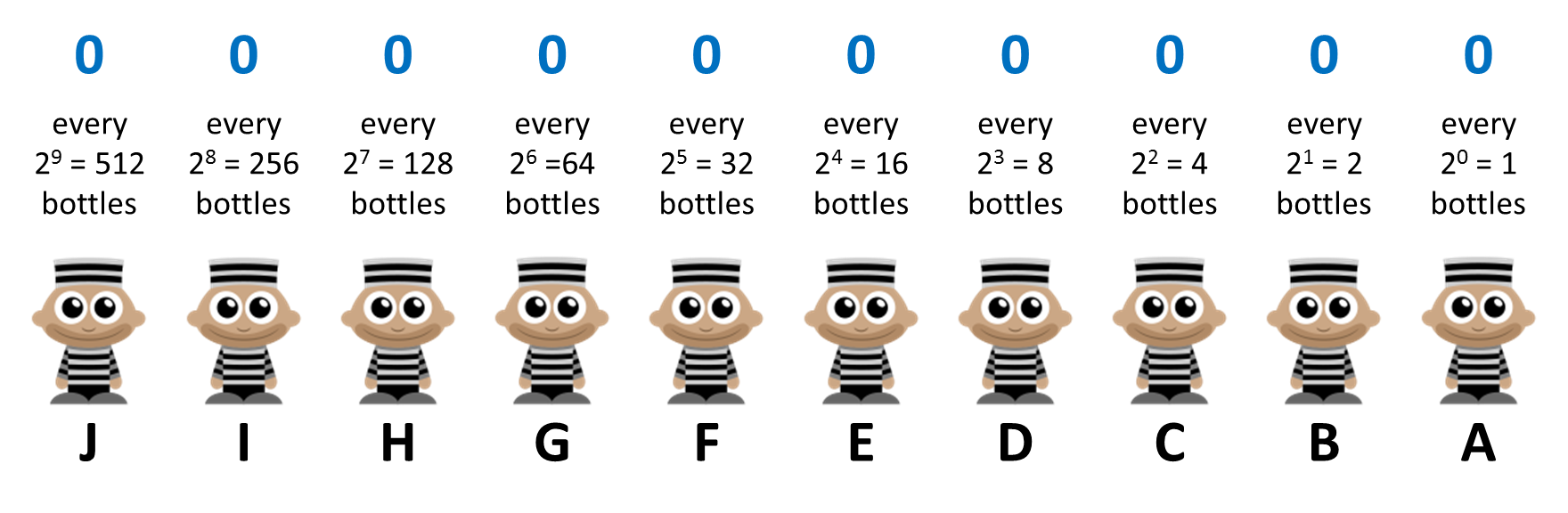
There we go. Let's first consider the case where none of the prisoners turns out to be dead after 24 hours? Which bottle of wine was poisoned? Well it must have been the first bottle (bottle #0), since this is the only bottle that none of them drank from. This is confirmed in our diagram because if none of the prisoners are poisoned, we place a zero above every one of them. And the number $$(0000000000)_2$$ in binary is still $$(0)_{10}$$ in decimal.

Now let's suppose that only prisoner A died after 24 hours. We place a one above prisoner A and a zero above the other prisoners.

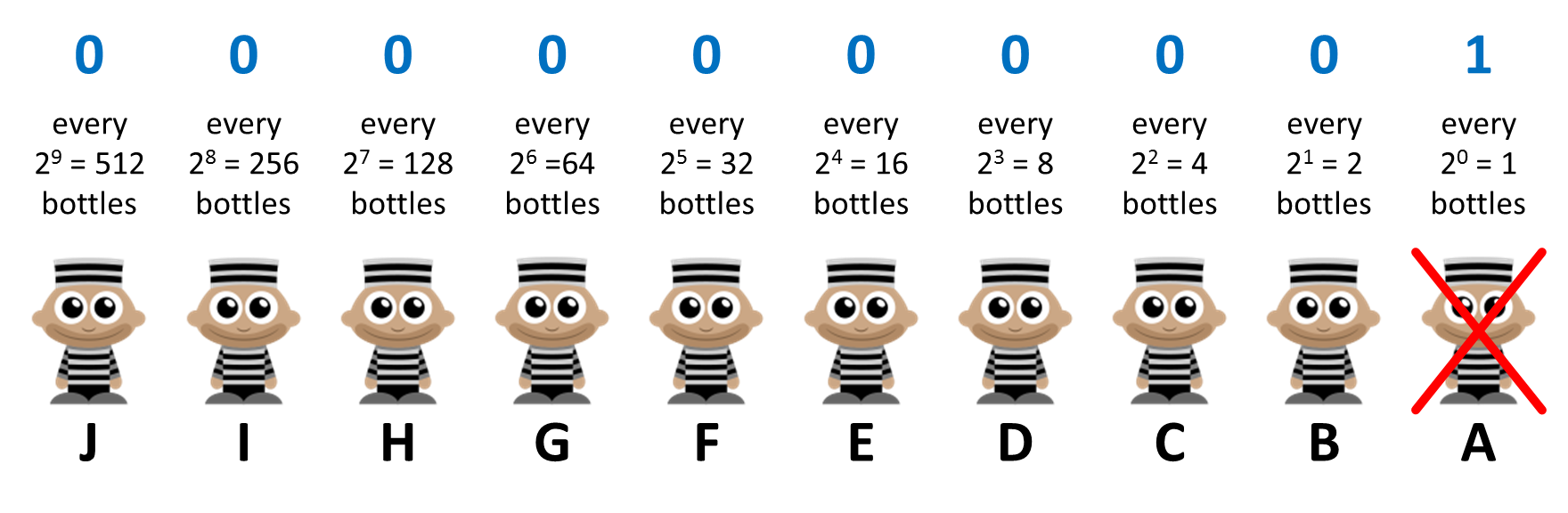
If we translate $$(0000000001)_2$$ into decimal we get $$(1)_{10}$$. Which means bottle #1 was poisoned. This confirms what we know to be true because prisoner A was the only prisoner who drank from bottle # 1 (remember prisoner A drank from bottles #1, #3, #5, …).

How about if prisoners A, C, E, G and I have died after 24 hours?

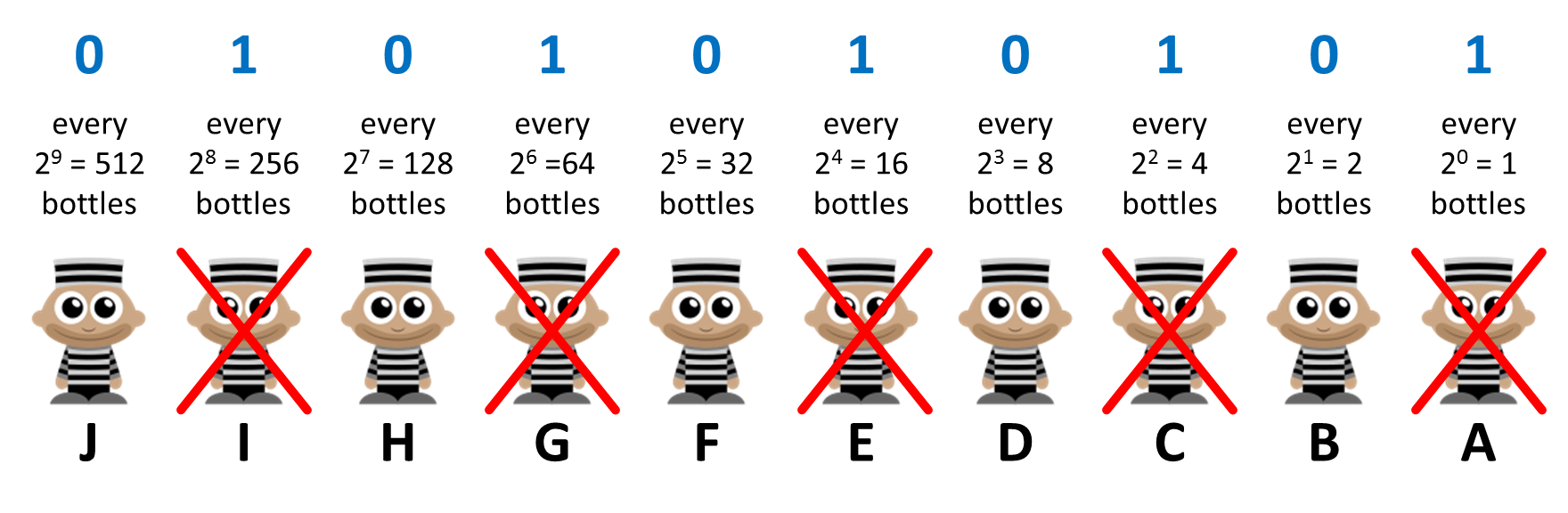
Translate the binary number $$(0101010101)_2$$ into decimal to determine which bottle was poisoned. \[(0101010101)_2 = 2^8 + 2^6 + 2^4 + 2^2 + 2^0 = 256 + 64 + 16 + 4 + 1 = 341\] Hence, bottle #341 was the poisonous bottle.

Pretty clever isn't it? Because there are 10 prisoners and each prisoner has two states (dead or alive), this system has a grand total of $$2^{10} = 1024$$ different combinations. This is more than enough combinations since we only have 1000 bottles.

Input

The first line of input contains a number $$n \in \mathbb{N}$$ that indicates how many prisoners have died after 24 hours. This is followed by the $$n$$ labels (capital letters) of the deceased prisoners, each on a separate line. These capital letters are not necessarily listed in alphabetic order.

Output

There is a single line of output that contains the text Bottle #n is poisoned., where n must be filled up with the number of the poisonous bottle.

Example

Input:

5
A
C
E
G
I

Output:

Bottle #341 is poisoned.