The Levenshtein distance between two DNA sequences is the minimal amount of treatments that are necessary in order to convert one sequence to another. This linear measure is named after Vladimir Levenshtein, who invented it in 1965. Apart from its use in the spelling checker, the Levenshtein disctance is also used to make astimates of the evolutionary distance betwee two DNA sequences (where the variants of the Needleman-Wunsh or the Smith-Waterman are usually used). Here, a DNA sequence can be represented by a sequence of symbols that consists only of the letters A, C, G and T. The collection of valid treatments is then insertion (inserting a letter), deletion (deleting a letter) and substitution (replacing a letter by another letter).

For the calculation of the Levenshtein distance between two given DNA sequences, a two-dimensional matrix $$d(0,\ldots,m;0,\ldots,n)$$ is used, where $$m$$ represents the length of the first DNA sequence and $$n$$ the length of the second DNA sequence. Initially you fill out the first column of the matrix $$d$$ with the numbers $$0,1,\ldots,m$$ and the first row with the numbers $$0,1,\ldots,n$$. The other numbers are calculated from left to right and from top to bottom, where the value on row $$i$$ and column $$j$$ are given by
\[ d_{i,j} = \textrm{minimum} \left\{ \begin{array}{ll} d_{i-1,j}+1&\textrm{deletion}\\ d_{i,j-1}+1&\textrm{insertion}\\ d_{i-1,j-1}+\textrm{cost}\quad\quad&\textrm{substitution}\\ \end{array} \right. \]
Here, the cost is equal to 0 if the $$i$$th letter of the first DNA sequence equals the $$j$$th letter of the second DNA sequence. Otherwise, the cost equals 1. At the end of this procedure, the Levenshtein distance can be read as the value on the bottom right of the matrix.

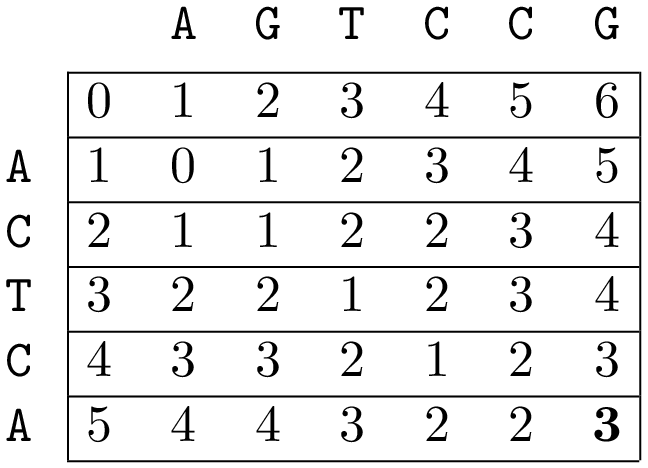
An example, the Levenshtein distance between ACTCA and AGTCCG is 3 and can thus be given: 

• ACTCA $$\longrightarrow$$ AGTCA (first C replaced by G)

• AGTCA $$\longrightarrow$$ AGTCC (A at the back replaced by C)

• AGTCC $$\longrightarrow$$ AGTCCG (add G in the back)

The end result after calculating the two-dimensional matrix $$d$$ looks as follows:

Assignment

Define a class Sequence which can be used to make instances of valid DNA sequences. The objects of the class Sequence must support the following methods:

• The initializing method __init__ allows to make DNA sequence objects based on a given string (that is given as an argument). Such objects have an attribute seq that refers to a string that only consists of the letters A, C, G and T. The given string must be converted by the method __init__ to upper case letters, and the validity of it must be checked by calling the initializing method validate. Study the example below to find out what must happen if the given string does not represent a valid DNA sequence.

• The method validate prints the value True if the value of the attribute seq only consists of the letters A, C, G and T. Otherwise, the value False is printed. To this method, no arguments must be given.

• The method distance prints the Levenshtein distance between the current Sequence object and another Sequence object that must be given to the method as an argument.

Example

>>> seq1 = Sequence('ACTCA')
>>> seq2 = Sequence('AGTCCG')
>>> seq1.distance(seq2)
3
>>> seq3 = Sequence('GTCNAAC')
Traceback (most recent call last):
AssertionError: invalid sequence