Vergelijken van twee groepen

Cholestorol voorbeeld

In een studie werd de cholestorolconcentratie in het bloed gemeten bij 5 patiënten (groep=1) die twee dagen geleden een hartaanval hadden en bij 5 gezonde personen (groep=2). De onderzoekers wensen na te gaan of de cholestorolconcentratie verschillend is bij hartpatiënten en gezonde personen. Boxplots en qqplots van de data worden weergegeven in Figuur 49 en 50.

chol <- read_tsv("https://raw.githubusercontent.com/statOmics/sbc20/master/data/chol.txt")

chol <- chol %>%
  mutate(group = as.factor(group))

nGroups <- chol %>%
  pull(group) %>%
  table

n <- nGroups %>%
  sum
chol

## # A tibble: 10 x 2
##    group cholest
##    <fct>   <dbl>
##  1 1         244
##  2 1         206
##  3 1         242
##  4 1         278
##  5 1         236
##  6 2         188
##  7 2         212
##  8 2         186
##  9 2         198
## 10 2         160

chol %>%  
  ggplot(aes(x=group,y=cholest)) +
  geom_boxplot(outlier.shape=NA) +
  geom_point(position="jitter")

Figuur 49: Boxplot van de cholesterol concentratie in het bloed bij hartpatiënten (groep 1) en gezonde individuen (groep 2). 

chol %>% ggplot(aes(sample=cholest)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(~group)

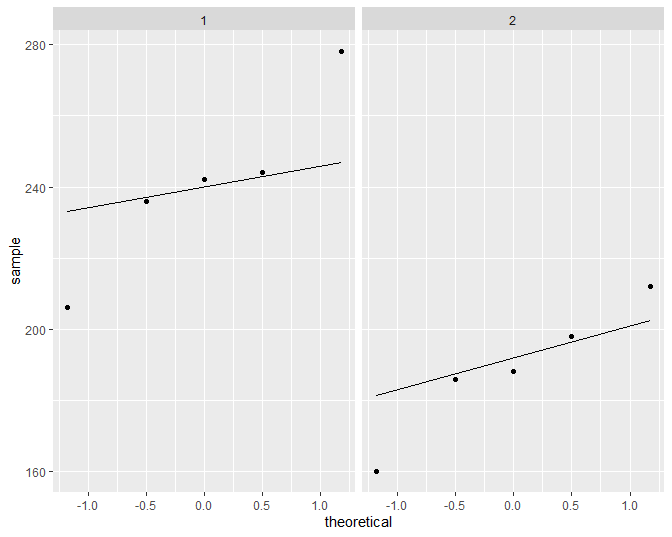
Figuur 50: Qqplot van de cholesterol concentratie in het bloed bij hartpatiënten (groep 1) en gezonde individuen (groep 2).

De boxplots en qqplots geven aan dat er mogelijks outliers in de data voorkomen. Het is moeilijk om inzicht te krijgen in de verdeling van de data gezien we maar 5 observaties hebben per groep.

Permutatietesten

De vraagstelling van het cholestorol voorbeeld is geformuleerd in erg ruime bewoordingen en dit laat vrijheid in de vertaling ervan naar een nulhypothese.

Laten we starten met een nulhypothese in termen van gemiddelden. Stel dat \(\mu_1\) en \(\mu_2\) de gemiddelde uitkomsten in behandelingsgroep 1 (hartpatiënten) en 2 (gezonde personen) voorstellen, dan zouden de hypotheses kunnen zijn:

\[H_0: \mu_1=\mu_2 \text{ versus } H_1: \mu_1\neq \mu_2.\]

Voor het testen van deze hypotheses kunnen we bijvoorbeeld gebruik maken van de two-sample \(t\)-test.

We gaan de voorwaarden na:

We kunnen dus de veronderstellingen van de two-sample \(t\)-test niet nagaan. We kunnen ook geen beroep doen op de asymptotische benadering omdat 5 observaties per groep te weinig is.

Samengevat: de veronderstellingen van de \(t\)-test kunnen niet worden nagegaan en er zijn te weinig observaties om gebruik te kunnen maken van de asymptotische benadering. Aangezien het erg gevaarlijk is een statistische methode te gebruiken waarvan de voorwaarden niet nagegaan kunnen worden, is de klassieke \(t\)-test niet de geschikte methode. De oplossing die in dit hoofdstuk besproken wordt, zijn permutatietesten. Om deze te kunnen beschrijven, zullen we eerst de nulhypothese anders formuleren.

Hypothesen

De oplossing die in deze sectie besproken wordt, zijn de permutatietesten. Om deze te kunnen beschrijven, zullen we eerst de nulhypothese anders formuleren.

De veronderstelling voor de two-sample \(t\)-test kunnen we als volgt schrijven, met \(Y_{1j}\) en \(Y_{2j}\) de notatie voor de uitkomsten uit respectievelijk groep 1 en 2:

\[Y_{1j} \text{ iid } N(\mu_1,\sigma^2) \;\;\;\text{ en }\;\;\; Y_{2j} \text{ iid } N(\mu_2,\sigma^2).\]

Onder \(H_0:\mu_1=\mu_2\), wordt dit (stel \(\mu=\mu_1=\mu_2\) onder \(H_0\))

\[Y_{ij} \text{ iid } N(\mu,\sigma^2),\]

wat uitdrukt dat alle \(n=n_1+n_2\) uitkomsten uit dezelfde normale distributie komen en onafhankelijk verdeeld zijn. Dit laat ons dus toe om de oorspronkelijke nulhypothese van de two-sample \(t\)-test anders te schrijven:

\[\begin{equation} H_0: F_1(y) = F_2(y) \text{ voor alle } y \;\;\;\text{ of }\;\;\; H_0: f_1(y) = f_2(y) \text{ voor alle } y \qquad(4) \end{equation}\]

met \(F_1\) en \(F_2\) de distributiefuncties en \(f_1\) en \(f_2\) de densiteitfuncties van de verdeling van de uitkomsten in respectievelijk behandelingsgroep 1 en 2, en met de bijkomende veronderstelling dat \(f_1\) en \(f_2\) de distributiefuncties van Normale verdelingen zijn.

Onder de alternatieve hypothese wordt een locatie-shift verondersteld:

\[H_1: f_1(y)=f_2(y-\Delta) \;\;\;\text{ voor alle } y\]

met \(\Delta=\mu_1-\mu_2\), verder hebben de Normale verdelingen dezelfde variantie.

We illustreren dit in R voor \(f_1\sim N(0,1)\) en \(f_2\sim N(1,1)\) en \(\Delta=-1\).

mu1 <- 0
sigma1 <- 1
mu2 <- 1
sigma2 <- 1
y <- -2:2
delta <- mu1 - mu2
delta

## [1] -1

dnorm(y, mu1, sigma1)

## [1] 0.05399097 0.24197072 0.39894228 0.24197072 0.05399097

dnorm(y - delta, mu2, sigma2)

## [1] 0.05399097 0.24197072 0.39894228 0.24197072 0.05399097

De permutatietesten die in de volgende sectie ontwikkeld worden, kunnen gebruikt worden voor het testen van de hypothese (4), maar dan zonder de Normaliteitsveronderstelling.

We schrijven hypothese (4) verkort als

\[H_0: F_1=F_2 \;\;\;\text{ of }\;\;\; H_0:f_1=f_2.\]

Als de nulhypothese waar is, met name dat de verdelingen van de cholestorolconcentraties gelijk zijn voor hartpatiënten en gezonde personen, dan zijn de groep-labels van de 10 personen niet informatief. Gezien er geen verschil is in de verdeling tussen beide groepen is elke groepering immers irrelevant. We kunnen bijgevolg de verdeling van de test-statistiek onder de nulhypothese bekomen door de groepslabels \(G\) te permuteren.

####Verdeling van de statistiek onder \(H_0\)

In praktijk zijn er \(m=\binom{n_1+n_2}{n_1}=\binom{n}{n_1}=\binom{n}{n_2}\) mogelijke unieke permutaties \(\cal{G}\) van de groepslabels. Voor ons voorbeeld zijn dat er \(m=\) 252. Als \(m\) niet te groot is dan kunnen alle unieke permutaties van de groepslabels berekend worden. Voor iedere unique permutatie \(g \in \cal{G}\) wordt de teststatistiek \(t^*_g\) berekend.

We kunnen alle m=252 permutaties in R genereren a.d.h.v. de functie combn(n,n_1). Dit wordt geïllustreerd in de onderstaande R code:

G <- combn(n,nGroups[1])
dim(G)

## [1]   5 252

G[,1:10]

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,]    1    1    1    1    1    1    1    1    1     1
## [2,]    2    2    2    2    2    2    2    2    2     2
## [3,]    3    3    3    3    3    3    3    3    3     3
## [4,]    4    4    4    4    4    4    5    5    5     5
## [5,]    5    6    7    8    9   10    6    7    8     9

De matrix G bevat voor elke permutatie de volgnummers van de observaties die tot de eerste groep zullen behoren. We tonen enkel de eerste 10 permutaties. We kunnen nu de teststatistiek berekenen voor de originele steekproef en voor elke permutatie

#Originele test statistiek
tOrig=t.test(cholest~group,chol)$statistic
#bereken alle permutatiecombinaties en voer voor
#elke combinantie een functie uit die de t-test statistiek
#berekent voor de gepermuteerde groepslabels
tOrig <- t.test(cholest ~ group, chol)$statistic
tOrig

##        t 
## 3.664425

tStar <- combn(
  n,
  nGroups[1],
	function(g,y) {
    t.test(y[g],y[-g])$statistic
    },
  y = chol %>% pull(cholest)
  )
head(tStar)

## [1] 3.6644253 1.6397911 2.3973923 1.5876250 1.9217173 0.9967105

length(tStar)

## [1] 252

Merk op dat y[g] de data selecteert met volgnummers g uit de vector y en y[-g] de data waarvoor de volgnummers niet tot g behoren. De vector tStar bevat de waarden van de teststatistiek \(t^*_g\) voor alle \(g \in {\cal{G}}\).

We kunnen nu de verdeling van de teststatistiek onder \(H_0\) bestuderen.

qplot(tStar,bins=50) +
  xlab(expression("permutatiestatistiek t"^"*")) +
  geom_vline(xintercept=tOrig,col=2)

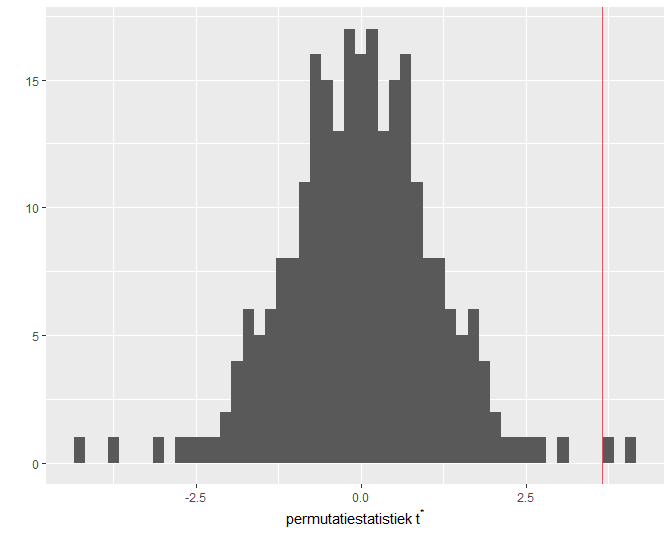
Figuur 51: Exacte permutatie nuldistributie van de Welch t-test voor het cholestorol voorbeeld. Bovenaan histogram van elke mogelijke waarde voor de test-statistiek. Onderaan een gewoon histogram met balkbreedtes gelijk aan 1. De geobserveerde waarde voor de test-statistiek is aangeduid met een rode verticale lijn.

Het histogram (Figuur 51) bevat alle informatie voor de permutatienuldistributie van de two-sample \(t\)-teststatistiek voor de geobserveerde uitkomsten; merk op dat er 2 unieke waarden van de teststatistiek berekend zijn.
Het histogram in Figuur 51 is de verdeling van de teststatistiek onder de nulhypothese. We zien eveneens dat de geobserveerde teststatistiek vrij extreem is.

p-waarde

Nu we in staat zijn de permutatienuldistributie te berekenen, kunnen we hypothesetesten uitvoeren net als in de parametrische statistiek. Voor een permutatietest is de \(p\)-waarde voor de tweezijdige test (immers \(H_1: \mu_1 \neq \mu_2\))

\[p=\text{P}_0\left[\vert T\vert \geq \vert t\vert \mid \mathbf{y}\right].\]

Merk op dat deze p-waarde geconditioneerd is op de geobserveerde cholestorolwaarden die weergegeven worden in de vector \(\mathbf{y}=(y_{11},\ldots,y_{51},y_{12},\ldots,y_{52})^T\).

Aangezien de permutatienuldistrubutie van \(T\) bepaald wordt door \(t^*_g\), \(g \in{\cal{G}}\), berekenen we

\[p = \text{P}_0\left[\left\vert T\right\vert \geq \left\vert t\right\vert \mid \mathbf{y}\right] = \frac{\#\{g\in {\cal{G}}: \vert t^*_g\vert \geq \vert t \vert \}}{m},\]

m.a.w. als de ratio van het aantal permutaties waarvoor de statistiek minstens even extreem is als de geobserveerde statistiek op het totaal aantal permutaties. In R kunnen we dit als volgt berekenen.

pval <- mean(abs(tStar)>=abs(tOrig))
pval

## [1] 0.01587302

We vinden dus een \(p\)-waarde van 0.0159. Aangezien \(p<5\%\), besluiten we op het \(5\%\) significantieniveau dat de distributies van de cholestorol concentraties niet gelijk zijn bij hartpatiënten en bij gezonde personen. De \(p\)-waarde die gevonden wordt via de permutatienuldistributie op basis van alle permutaties wordt een exacte \(p\)-waarde genoemd. De permutatienuldistributie wordt een exacte nuldistributie genoemd. De term exact betekent dat de resultaten correct zijn voor iedere steekproefgrootte \(n\).

De kans op een type I fout wordt dus gecontroleerd door een permutatietest, maar wel conditioneel op de geobserveerde uitkomsten data \(\mathbf{y}\).

We hebben steeds geconditioneerd op de observaties van de steekproef. We kunnen ons nu afvragen of we de conclusies kunnen veralgemenen naar de populatie toe? Het antwoord is ja, als de subjecten at random getrokken zijn uit de populatie. Het bewijs hiervan valt buiten het bestek van de cursus.

Soms treedt er een praktisch probleem op omdat het aantal permutaties \(m=\#{\cal{G}}\) erg groot is. Enkele voorbeelden: \(\binom{20}{10}=\) 184756, \(\binom{30}{15}=\) 1.55e+08 en \(\binom{40}{20}=\) 1.38e+11.

Dus zelfs met slechts 40 observaties en een gebalanceerde proefopzet is het quasi onmogelijk om alle permutaties één voor één door te rekenen. De oplossing bestaat erin om niet alle \(g \in {\cal{G}}\) te beschouwen, maar slechts een beperkt aantal (bv. 10000 of 100000). We kunnen m.a.w. de nuldistributie benaderen door een groot aantal random permutaties uit te voeren.

Hoe kunnen we conclusie interpreteren

We permuteren immers t statistiek. De effectgrootte in de t-test is de locatie-shift.

Als locatie-shift model niet opgaat is een significant resultaat moeilijk te interpreteren. Het is dan immers niet duidelijk tegenover welk alternatief we dan testen.

Locatie-shift kan niet worden nagegaan in kleine steekproeven…