The letters of a word are loaded onto a train one by one (from left to right), where

• the letter A weighs 1 ton

• the letter B weighs $$\frac{1}{2}$$ ton

• the letter C weighs $$\frac{1}{3}$$ ton

• …

• the letter Z weighs $$\frac{1}{26}$$ ton

Each wagon has a maximum load capacity of 1 ton. A next wagon is only mounted if the next letter can no longer be loaded on the current wagon without exceeding the maximum load capacity.

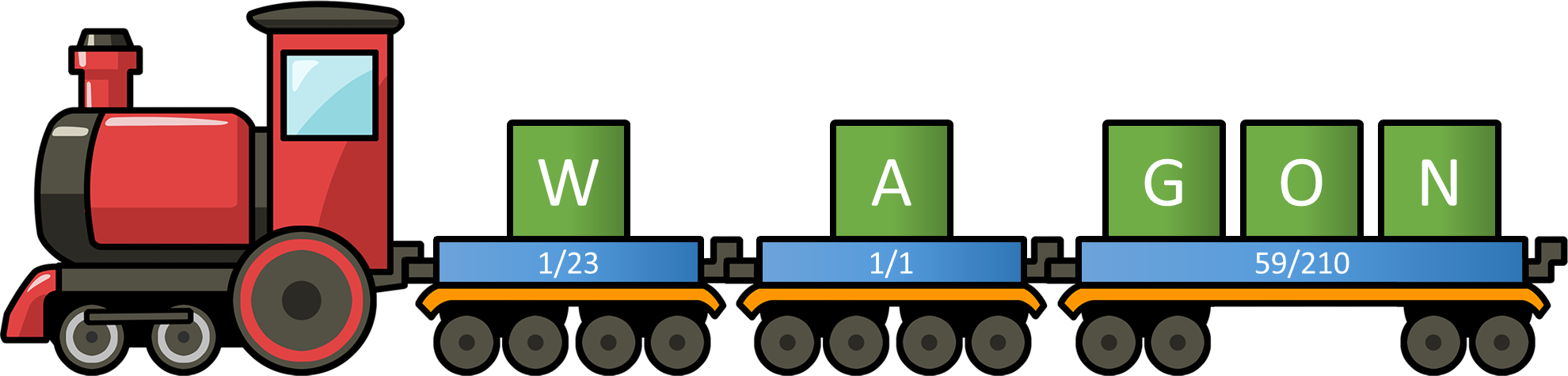
Above you see, for example, how the letters of the word WAGON are loaded onto a train. For each wagon we have indicated the total weight of its cargo. The first letter is W and weights $$\frac{1}{23}$$ ton. The second letter is A and weighs 1 ton. The letter A doesn't fit on the first wagon anymore, otherwise it would become too heavily loaded. As such, a second wagon is mounted to carry the letter A. Because this wagon is fully loaded right away, a third wagon is mounted. This wagon can carry the remaining letters G, O and N, because together they weigh (in tons) \[ \frac{1}{7} + \frac{1}{15} + \frac{1}{14} = \frac{59}{210} \]

Assignment

A word is represented as a string (str) that only contains letters. A fraction is represented as a Fraction — a data type defined in the module fractions¹ of the Python Standard Library². Your task:

• Write a function weight that takes a letter (str). The function must return the weight (Fraction) of the given letter (in tons).

• Write a function fracture that takes a word $$w$$ (str). The function must return the fracture of $$w$$ — a tuple containing the weights (Fraction) of the wagons that are successively loaded with the letters of $$w$$.

• Write a function refractions that takes the location (str) of a text file containing a sequence of words, each on a separate line. The function must return the refractions of the words — a dictionary (dict) whose keys are the fractures of all words in the given file. The dictionary must map each fracture onto the set of all words (str, in uppercase) in the given file with that fracture.

• Write a function diffractions that takes two arguments: i) a word $$w$$ (str) and ii) the refractions $$r$$ (dict) of a sequence of words. The function must return the set of all words (str, in uppercase) in $$r$$ with the same fracture as $$w$$. However, the word $$w$$ itself may not appear in the set returned by the function.

None of these functions may make a distinction between uppercase and lowercase letters.

Example

In the following interactive session we assume the text file words.txt³ to be located in the current directory.

>>> weight('A')
Fraction(1, 1)
>>> weight('c')
Fraction(1, 3)
>>> weight('Z')
Fraction(1, 26)

>>> fracture('WAGON')
(Fraction(1, 23), Fraction(1, 1), Fraction(59, 210))
>>> fracture('Cortisone')
(Fraction(6443, 7980), Fraction(1, 5))
>>> fracture('destruct')
(Fraction(1184, 1197), Fraction(1, 20))
>>> fracture('hindsight')
(Fraction(1184, 1197), Fraction(1, 20))

>>> refraction = refractions('words.txt4')
>>> refraction[(Fraction(1, 23), Fraction(1, 1), Fraction(59, 210))]
{'WAGON'}
>>> refraction[(Fraction(6443, 7980), Fraction(1, 5))]
{'CORTISONE', 'ENCLOSE'}
>>> refraction[(Fraction(1184, 1197), Fraction(1, 20))]
{'DESTRUCT', 'HINDSIGHT', 'RUSTBELT'}

>>> diffractions('WAGON', refraction)
set()
>>> diffractions('Cortisone', refraction)
{'ENCLOSE'}
>>> diffractions('destruct', refraction)
{'HINDSIGHT', 'RUSTBELT'}
>>> diffractions('hindsight', refraction)
{'DESTRUCT', 'RUSTBELT'}

Resources

• General Intelligence and Security Service (2014). End of year puzzle 2014, assignment 7.