Forget everything you know about reducing fractions — it turns out you can just cancel common digits of the numerator and denominator:

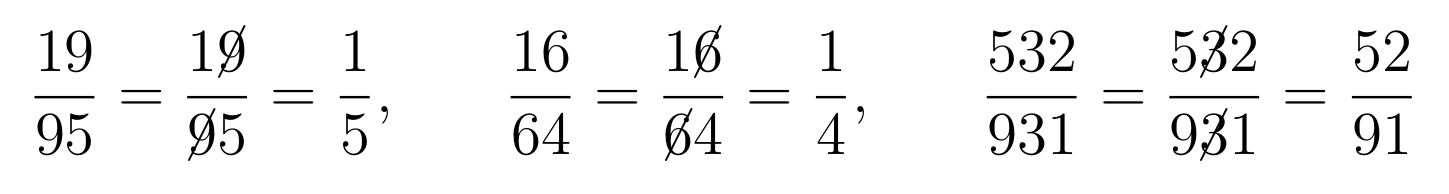
Not convinced? Then there's nothing wrong with your gut feeling! The above fractions are just a couple of special cases for which the cancelling procedure (which we will refer to as reductio ad absurdum) results in an equivalent fraction. Applied to most other fractions, the procedure results in a different value. Try it out, for example, on the fraction $$\frac{12}{13}$$.

Assignment

Your task is to check whether it is allowed to apply the reductio ad absurdum technique to a given fraction. To do this, just follow these steps:

• Write a function equivalentFraction that takes four integers $$n_1, d_1, n_2, d_2 \in \mathbb{N}_0$$. The function must return a boolean value that indicates whether or not the fractions $$\frac{n_1}{d_1}$$ and $$\frac{n_2}{d_2}$$ are equivalent. Note that it is better to avoid using floating point division when testing the equivalence, due to possible rounding errors. Instead, it is better to give both fractions a common denominator and then compare their numerators.

• Write a function reduction that takes two integers $$n, d \in \mathbb{N}_0$$ which respectively represent the numerator and denominator of a fraction. For each common digit of the numerator and denominator, cancel its leftmost occurrence in both the numerator and denominator, until the numerator and denominator have no more digits in common. The function must return two integers that respectively represent the numerator and denominator that result after cancelling the common digits. If all digits of the numerator have been cancelled, the first value returned must be -1. Similar, the second value returned should be -1 if all digits of the denominator have been cancelled.

• Use the functions equivalentFraction and reduction to write a function validReduction that takes two integers $$n, d \in \mathbb{N}_0$$ which respectively represent the numerator and denominator of a fraction. The function validReduction must return the same value as the function reduction in case the reduced fraction turns out to be valid. The latter is the case if the following conditions are fulfilled:

• both the numerator and denominator contain at least one digit after reduction

• the denominator is different from zero after reduction (division by zero is invalid)

• the reduced fraction is equivalent to the original fraction before reduction (sensu the definition of equivalence as implemented by the function equivalentFraction)

In case reduction would result in an invalid fraction, the function validReduction must return te original numerator and denominator that were passed as arguments to the function.

Example

>>> equivalentFraction(19, 95, 1, 5)
True
>>> equivalentFraction(532, 931, 52, 91)
True
>>> equivalentFraction(12, 13, 2, 3)
False

>>> reduction(19, 95)
(1, 5)
>>> reduction(532, 931)
(52, 91)
>>> reduction(2349, 9396)
(24, 96)
>>> reduction(12, 13)
(2, 3)
>>> reduction(11, 10)
(1, 0)
>>> reduction(123, 3214)
(-1, 4)

>>> validReduction(19, 95)
(1, 5)
>>> validReduction(532, 931)
(52, 91)
>>> validReduction(2349, 9396)
(24, 96)
>>> validReduction(12, 13)
(12, 13)
>>> validReduction(11, 10)
(11, 10)
>>> validReduction(123, 3214)
(123, 3214)