A picture often says more than a thousand words. That is literally the case for this photograph.

William Frederick Friedman¹ — the father of modern American cryptology — was fond of a cipher² devised by Francis Bacon³. A scheme so flexible that it could hide a message in a drawing, a piece of sheet music, almost any imaginable setting. Bacon himself described it as "anything can be made to signify anything".

Friedman (at the far right of the 5 black-clad persons in the center of the photo) used the cipher in 1918 to hide a message in the graduation photograph of the code-breakers' class that he'd taught with his wife Elizebeth (in the center of the 5 black-clad persons in the center of the photo) to a group of soldiers from the U.S. Army⁴. If you look more closely, you'll notice that some soldiers are either facing forward towards the camera, while others are facing to the side.

In doing that, they're encoding the message KNOWLEDGE IS POWER, a quotation of Bacon's that was a favorite of Friedman's. But apparently the first soldier in the last W-group was facing the wrong way (he should have looked sideways instead of straight into the camera) and there weren't enough people to complete the R-group.

Friedman kept the photo on his desk for the rest of his career, and when he died in 1969 Elizebeth had the phrase engraved on his tombstone in a design of her own devising:

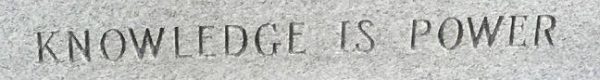
In 2017, cryptographer Elonka Dunin⁵ noticed that the inscription is composed of both serif⁶ and sans-serif⁷ letters. It turns out that even this is a cipher — Elizabeth had used it to conceal the letters WFF, William's initials. Dunin calls it "a fitting tribute, in the life of a couple who had been so dedicated to the field of codes and ciphers."

Assignment

In Bacon's cipher, each plaintext⁸ symbol is represented by a pattern of five a's and b's in the ciphertext⁹. Because $$2^5 = 32$$ different patterns can be formed in total, 32 different symbols can be encoded. We will record the key of the cipher in a text file with 32 lines. Each line of the file consists of one symbol (one character), followed by a tab and the unique pattern that encodes the symbol. This is an example of such a text file (key.txt¹⁰):

A	aaaaa
B	aaaab
C	aaaba
D	aaabb
E	aabaa
F	aabab
G	aabba
H	aabbb
I	abaaa
K	abaab
…
 	bbaba
.	bbabb
,	bbbaa
'	bbbab
?	bbbba
!	bbbbb

To encode the plaintext KNOWLEDGEISPOWER using Bacon's cipher, we simply replace each symbol with its corresponding pattern:

abaab abbaa abbab babaa ababa aabaa aaabb aabba
  K     N     O     W     L     E     D     G

aabaa abaaa baaab abbba abbab babaa aabaa baaaa
  E     I     S     P     O     W     E     R

This way, the length of the ciphertext is always a multiple of five. However, it is also allowed to omit at most four a's at the end of the ciphertext. So this is also a valid ciphertext for the plaintext KNOWLEDGEISPOWER (four a's omitted at the end):

abaababbaaabbabbabaaababaaabaaaaabbaabbaaabaaabaaabaaababbbaabbabbabaaaabaab

If the length of the ciphertext is not a multiple of five, then it can be supplemented at the end with one to four a's to arrive at a length that is a multiple of five. We may then decode the ciphertext by replacing each pattern of five a's and b's with the corresponding plaintext symbol.

An encoded message that would always be represented as a sequence containing only a's and b's would immediately indicate that Bacon's cipher is used. To obscure the fact that some representation contains an encoded message, $$a$$ and $$b$$ may also represent two different classes: letters that look different (different fonts; bold vs plain text), different kinds of musical notes, or people looking towards the camera in different ways.

In this assignment we will use two separate groups of characters to represent the classes $$a$$ and $$b$$ in the ciphertext. If we use lowercase letters for character class $$a$$ and uppercase letters for character class $$b$$, then the plaintext KNOWLEDGEISPOWER could for example be encoded as:

tZsyFqBHyprHDoMVhVzkhVfGgeyVqvvjbDTfkRLmsgEgkvKforNmjiXhRLDwgSKnMFpQutrcCbeUwrzf

If character class $$a$$ is represented by people looking straight at the camera (=) and character class $$b$$ by persons looking left (<) or right (>), the same plaintext could for example be encoded as:

=>==>=>>===>>=>>=>===<=<===<=====<<==>>===>===>===>===<=<<<==<<=<<=<====>==<====

Define a class Bacon to represent codecs that can encode and decode messages using Bacon's cipher with a given key. When creating a new codec (Bacon), the location (str) of a text file with the cipher's key must be passed. A codec (Bacon) must support at least the following methods:

• A method encode_visible that takes a plaintext (str) and returns the corresponding ciphertext in which each pattern is represented as a sequence of five a's and b's.

• A method decode_visible that takes a ciphertext (str) in which each pattern is represented as a sequence of five a's and b's. At most four a's may have been omitted at the end of the ciphertext. The method must return the corresponding plaintext.

• A method encode_hidden that takes a plaintext (str). The method also has two optional parameters a and b that can be used to specify which groups of characters represent the character classes $$a$$ and $$b$$ in the ciphertext. The parameter a (resp. b) can take a string (str) containing all characters that represent character class $$a$$ (resp. $$b$$). If no value is explicitly passed to parameter a (resp. b), then character class $$a$$ (resp. $$b$$) consists of all lowercase letters (resp. uppercase letters). The method must return the corresponding ciphertext in which each pattern is represented as a sequence of five characters. Each of these characters must be chosen at random from all possible characters in character class $$a$$ (parameter a) or character class $$b$$ (parameter b).

• A method decode_hidden that takes a ciphertext (str) in which each patten is represented as a sequence of five characters from character classes $$a$$ and $$b$$. The method also has two optional parameters a and b that can be used to specify which groups of characters represent the character classes $$a$$ and $$b$$ in the ciphertext, in the same way as with method encode_hidden. At most four characters from character class $$a$$ may have been omitted at the end of the ciphertext. The method must return the corresponding plaintext.

This class and all its methods may assume that only valid keys, plaintexts, and ciphertexts are passed, without the need to check this explicitly.

Example

In the following interactive session we assume that the text file key.txt¹¹ is located in the current directory.

>>> codec = Bacon('key.txt12')

>>> codec.encode_visible('F')
'aabab'
>>> codec.encode_visible('W')
'babaa'
>>> codec.encode_visible('WFF')
'babaaaababaabab'
>>> codec.encode_visible('KNOWLEDGEISPOWER')
'abaababbaaabbabbabaaababaaabaaaaabbaabbaaabaaabaaabaaababbbaabbabbabaaaabaabaaaa'

>>> codec.decode_visible('aabab')
'F'
>>> codec.decode_visible('bab')
'W'
>>> codec.decode_visible('babaaaababaabab')
'WFF'
>>> codec.decode_visible('abaababbaaabbabbabaaababaaabaaaaabbaabbaaabaaabaaabaaababbbaabbabbabaaaabaab')
'KNOWLEDGEISPOWER'

>>> codec.encode_hidden('F')
'chLqM'
>>> codec.encode_hidden('W', a='=', b='<>')
'<=>=='
>>> codec.encode_hidden('WFF')
'RkUkjvvVcNuqKkE'
>>> codec.encode_hidden('KNOWLEDGEISPOWER')
'tZsyFqBHyprHDoMVhVzkhVfGgeyVqvvjbDTfkRLmsgEgkvKforNmjiXhRLDwgSKnMFpQutrcCbeUwrzf'
>>> codec.encode_hidden('KNOWLEDGEISPOWER', a='=', b='<>')
'=>==>=>>===>>=>>=>===<=<===<=====<<==>>===>===>===>===<=<<<==<<=<<=<====>==<===='

>>> codec.decode_hidden('chLqM')
'F'
>>> codec.decode_hidden('<=>', a='=', b='<>')
'W'
>>> codec.decode_hidden('RkUkjvvVcNuqKkE')
'WFF'
>>> codec.decode_hidden('tZsyFqBHyprHDoMVhVzkhVfGgeyVqvvjbDTfkRLmsgEgkvKforNmjiXhRLDwgSKnMFpQutrcCbeU')
'KNOWLEDGEISPOWER'
>>> codec.decode_hidden('=>==>=>>===>>=>>=>===<=<===<=====<<==>>===>===>===>===<=<<<==<<=<==<====>==<', a='=', b='<>')
'KNOWLEDGEISPOEER'

Epilogue

William Friedman (1891–1969) received a degree in genetics from Cornell University¹³ before he started a carreer as a cryptologist in the U.S. Army. It therefore does not come as a surprise that he used a picture of a sunflower to illustrate how words can be hidden using Bacon's cipher.

It gets even worse when we look at the following picture of a castle.

This is not easy to decipher, even if you know that it contains an encrypted message. The stones with and without shadow encode this text:

My business is to write prescriptions
And then to see my doses staken
But now I find I spend my time
Endeavoring to out-Bacon Bacon

And finally, the caption at the bottom of this music score tips us off to the Baconian cipher it contains.

This time Friedman left no key. However, once you realize that some musical notes have an intact stem (class $$a$$) where others have a broken stem (class $$b$$), it does not take long to extract the secret message: ENEMY ADVANCING RIGHT / WE MARCH AT DAYBREAK.

Epilogue

Resources

• Dunin E (2017). Cipher on the William and Elizebeth Friedman tombstone at Arlington National Cemetery is solved. ¹⁴

• Goldman IL (2017). William Friedman, Geneticist Turned Cryptographer. Genetics 206(1), 1–8. ¹⁵

• NSA Center for Cryptologic History (2006). The Friedman Legacy: A Tribute to William and Elizebeth Friedman. ¹⁶