Take any random bitstring containing a sequence of $$m \in \mathbb{N}_0$$ zeros and ones. Place the zeros and ones of the bitstring clockwise around a circle. Reproduce the circle a second time, concentrically with the first circle. Rotate the inner circle over $$n \in \mathbb{Z}$$ places. If $$n > 0$$ the inner circle is rotated clockwise over $$n$$ places. If $$n < 0$$ the inner circle is rotated counterclockwise over $$|n|$$ places.
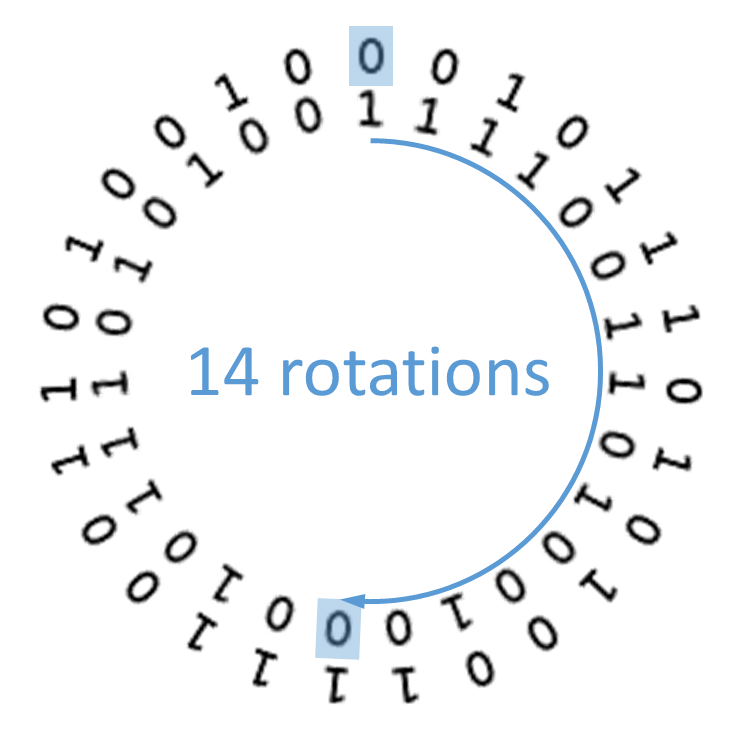
Now count the number of places where both circles have a zero opposite a one.
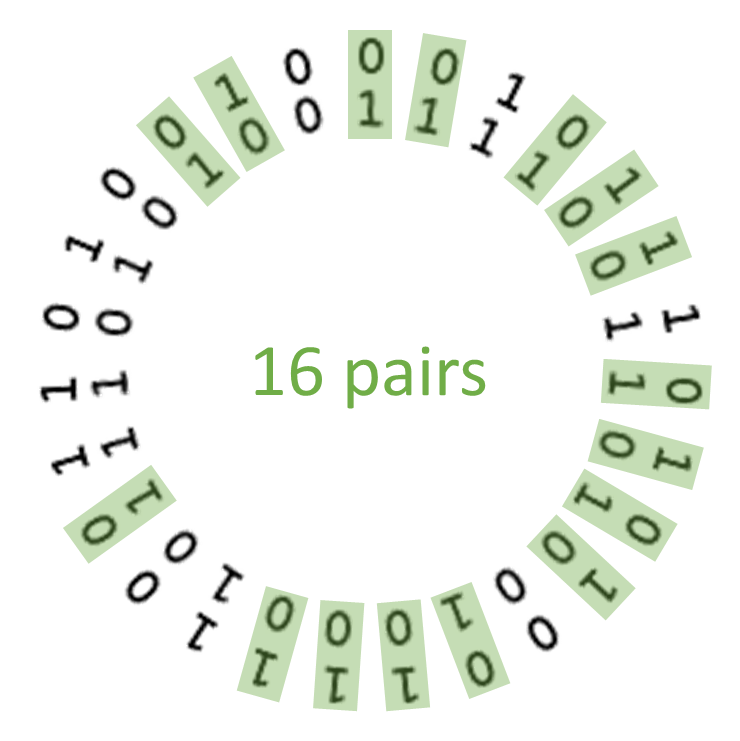
This will always yield an even number.
Input
A line containing a bitstring that exists of $$m \in \mathbb{N}_0$$ successive zeros and ones, followed by another line containing a number $$n \in \mathbb{Z}$$.
Output
A line containing the given bitstring, followed by a line containing the given bitstring that is rotated over $$n$$ places. In between these two lines is another line that marks each of the $$m$$ corresponding places with vertical bars (|) where zeros are opposite ones or with spaces where this is not the case. Following these $$m$$ vertical bars and spaces is another space and between round brackets the number of places where zeros are opposite ones.
Example
Input:
001011101010011110011010010
14Output:
001011101010011110011010010
|| ||| |||| |||| | || (16)
111100110100100010111010100