Facing dental surgery one day, mathematician Matt Parker1 asked Twitter for a math puzzle to distract him. One of his friends tweeted the following challenge:
Arrange the digits 1 to 9 in order so that the first two digits form a multiple of 2, the first three digits form a multiple of 3, the first four digits form a multiple of 4 etc. and finally the entire number is a multiple of 9.
Leaving the digits in the conventional order 123456789 doesn't work: 12 is divisible by 2 and 123 by 3, but 1234 isn't evenly divisible by 4. Matt Parker said:
By the end of my dental procedure, I had some but not all of the digits worked out, but, apparently, you're not allowed to stay in the dentist's chair after they're finished.
At home he finished working out the solution, which is unique. What is it?
Assignment
The above puzzle can be generalized by dropping the condition that each digit between 1 and 9 needs to occur just once. We say that a natural number with digits abcde… is polydivisible if it has the following properties:
-
its first digit a is not 0 (in other words: the number has no leading zeros)
-
the number formed by its first two digits ab is a multiple of 2
-
the number formed by its first three digits abc is a multiple of 3
-
the number formed by its first four digits abcd is a multiple of 4
-
and so on
For example, 345654 is a six-digit polydivisible number, but 123456 is not a polydivisible number, because 1234 is not a multiple of 4. In total there are 2492 nine-digit polydivisible numbers, but the only one that satisfies the additional condition from the puzzle is 381654729. Your task:
-
Write a function longest_polydivisible_prefix that takes an integer (int) $$n \in \mathbb{N}_0$$. The function must return the longest polydivisible prefix of $$n$$ (int). A prefix of a number is a sequence of successive leading digits of the number: 12345 is a prefix of 123456789, but 4567 or 789 are not.
-
Write a function ispolydivisible that takes an integer (int) $$n \in \mathbb{N}_0$$. The function must return a Boolean value (bool) that indicates if $$n$$ is polydivisible.
-
Write a function polydivisible_extensions that takes an integer (int) $$n \in \mathbb{N}_0$$. The function must return how many (int) polydivisible numbers we may obtain by appending an extra digit (0 through 9) at the end of $$n$$. As such, 12 has four polydivisible extensions: 120, 123, 126 and 129.
Example
>>> longest_polydivisible_prefix(1234356789)
123
>>> longest_polydivisible_prefix(381654729)
381654729
>>> longest_polydivisible_prefix(381654728)
38165472
>>> ispolydivisible(1234356789)
False
>>> ispolydivisible(381654729)
True
>>> ispolydivisible(381654728)
False
>>> polydivisible_extensions(12)
4
>>> polydivisible_extensions(23)
0
>>> polydivisible_extensions(381654729)
1
Epilogue
How many polydivisible numbers are there? If $$n$$ is a polydivisible number with $$k - 1$$ digits, then it can be extended to create a polydivisible number with $$k$$ digits if there is a number between $$10n$$ and $$10n + 9$$ that is divisible by $$k$$. If $$k$$ is less or equal to 10, it is always possible to extend an $$k - 1$$ digit polydivisible number to a $$k$$-digit polydivisible number in this way, and indeed there may be more than one possible extension. If $$k$$ is greater than 10, it is not always possible to extend a polydivisible number in this way, and as $$k$$ becomes larger, the chance of being able to extend a given polydivisible number become smaller.
On average, each polydivisible number with $$k - 1$$ digits can be extended to a polydivisible number with $$k$$ digits in $$\frac{10}{k}$$ different ways. This leads to the following estimate of the number of $$k$$-digit polydivisible numbers, which we will denote by $$F(k)$$: \[ F(k) \approx \frac{9 \times 10^{k - 1}}{k!} \] Summing over all values of $$k$$, this estimate suggests that the total number of polydivisible numbers will be approximately \[ \frac{9 \times (e^{10} - 1)}{10} \approx 19823 \] In fact, this underestimates the actual number of polydivisible numbers by about 3%. We can find the actual values of $$F(k)$$ by counting the number of polydivisible numbers with a given length:
| $$k$$ | $$F(k)$$ | estimate of $$F(k)$$ |
|---|---|---|
| 1 | 9 | 9 |
| 2 | 45 | 45 |
| 3 | 150 | 150 |
| 4 | 375 | 375 |
| 5 | 750 | 750 |
| 6 | 1200 | 1250 |
| 7 | 1713 | 1786 |
| 8 | 2227 | 2232 |
| 9 | 2492 | 2480 |
| $$k$$ | $$F(k)$$ | estimate of $$F(k)$$ |
|---|---|---|
| 10 | 2492 | 2480 |
| 11 | 2225 | 2255 |
| 12 | 2041 | 1879 |
| 13 | 1575 | 1445 |
| 14 | 1132 | 1032 |
| 15 | 770 | 688 |
| 16 | 571 | 430 |
| 17 | 335 | 253 |
| 18 | 180 | 141 |
| $$k$$ | $$F(k)$$ | estimate of $$F(k)$$ |
|---|---|---|
| 19 | 90 | 74 |
| 20 | 44 | 37 |
| 21 | 18 | 17 |
| 22 | 12 | 8 |
| 23 | 6 | 3 |
| 24 | 3 | 1 |
| 25 | 1 | 1 |
The distribution of polydivisible numbers can also be represented in a graphical way:
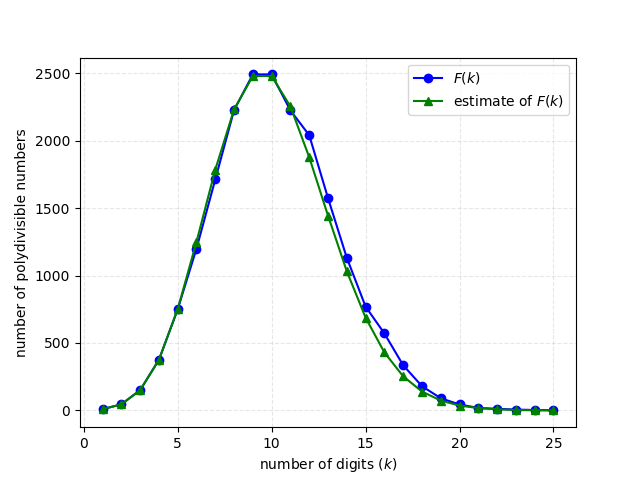
There are 20456 polydivisible numbers altogether, and the longest polydivisible number — having 25 digits — is:
3608528850368400786036725
Apart from the condition imposed in the puzzle in the introduction of this assignment, we can also search for polydivisible numbers with alternative restrictions on the digits. For example, the longest polydivisible number that only uses even digits is
48000688208466084040
We can also search for polydivisible numbers that are palindromes. The longest palindromic polydivisible number is
30000600003