The Game of Life, is a game devised by the British mathematician John Horton Conway in 1970. The game made its first public appearance in the October 1970 issue of Scientific American1, in Martin Gardner's "Mathematical Games" column. This type of game is an example of a cellular automaton, and differs from other games like Monopoly, Risk or chess, in the sense that there are no players and that one cannot win or lose.
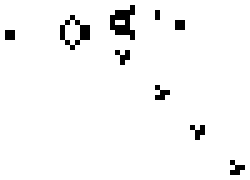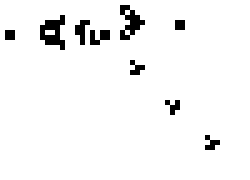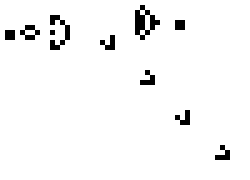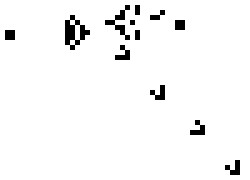
The game board consists of a rectangular grid, and can thus be represented by a list of lists in a computer program. After a number of cells of the grid are colored, the game begins. Game of Life goes through several "generations". In order to determine whether a cell is colored in the next generation or not, a number of rules are applied on the basis of the status (alive or dead) of the neighbours. Each cell in the grid has up to 8 neighbours, except the cells at the edge of the grid that have less than 8 neighbours. Conway has experimented with a lot with different sets of rules to find a good balance. With the wrong rules more squares (in Game of Life called "cells")would be coloured ('born') than white ("dead ") so the whole board ('grid') would be coloured. Or vice versa: there are so many fields death that the whole area goes white. The rules most commonly used are the following:
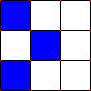
Any live cell with two or three live neighbours lives on to the next generation, like the middle cell in the image below. In this example, the center cell remains coloured, because the cell is surrounded by two other coloured cells.
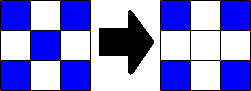
Any live cell with more than three live neighbours dies, as if by overcrowding (that means the cel goes white). Any live cell with fewer than two live neighbours diesas well, as if caused by under-population. This is illustrated in the figure below. In this example, the center cell dies, because the cell is surrounded by more than 3 or less than 2 coloured cells.
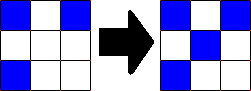
Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction, as shown in the figure below. In this example, the center cell is coloured, because the cell is surrounded by exactly 3 coloured cells.
All of these transformations are carried out simultaneously for all the cells. The art of the game is to imagine patterns that exhibit particular behaviour. There are stable patterns (simplest example: a block of four). There are patterns that go back and forth between two or more states. There are patterns that eventually disappear or change into a stable pattern. Interesting the patterns are those that move, such as the glider and the glider gun.
Assignment
Write a function showGeneration that prints the state of a given generation. This function has one required argument: a list of lists that represents a rectangular grid. The nested lists each have the same length and only contain Boolean values. A generation is thus represented by a list of rows, and each row itself is represented through a list. At position $$n$$ there is True if the cell in column $$n$$ in that row is alive. Otherwise there is False. The living cells are represented by the letter X when printing, and the dead cells are represented by the letter O (not the number zero !!).
Write a function numberOfNeighbours that returns the number of live neighbours of a cell for a given generation and a given cell. This function has three mandatory arguments: the first argument is the given generation, the second argument the row and the third argument the column of the cell of which the neighbours are sought.
Use the numberOfNeighbours function to write nextGeneration, a function that returns the next generation of a given generation. This new generation is presented in the same way as the given generation, namely, as a list of lists. The given generation is passed as an argument to the function, and is not changed by the function.
Example
>>> generation = [[True] + [False] * 7 for _ in range(6)]
>>> showGeneration(generation)
X O O O O O O O
X O O O O O O O
X O O O O O O O
X O O O O O O O
X O O O O O O O
X O O O O O O O
>>> numberOfNeighbours(generation, 0, 0)
1
>>> numberOfNeighbours(generation, 1, 1)
3
>>> numberOfNeighbours(generation, 2, 2)
0
>>> next = nextGeneration(generation)
>>> showGeneration(next)
O O O O O O O O
X X O O O O O O
X X O O O O O O
X X O O O O O O
X X O O O O O O
O O O O O O O O
>>> next = nextGeneration(next)
>>> showGeneration(next)
O O O O O O O O
X X O O O O O O
O O X O O O O O
O O X O O O O O
X X O O O O O O
O O O O O O O O
>>> next = nextGeneration(next)
>>> showGeneration(next)
O O O O O O O O
O X O O O O O O
O O X O O O O O
O O X O O O O O
O X O O O O O O
O O O O O O O O
>>> next = nextGeneration(next)
>>> showGeneration(next)
O O O O O O O O
O O O O O O O O
O X X O O O O O
O X X O O O O O
O O O O O O O O
O O O O O O O O