Floyd’s algorithm uses dynamic programming to calculate the shortest path between every pair of nodes simultaneously. We start with an adjacency list adj, containing all weights between all nodes, or inf if there is no edge between 2 nodes.

dist ← adj
for k from 1 to |dist|
   for i from 1 to |dist|
      for j from 1 to |dist|
         if dist[i][j] > dist[i][k] + dist[k][j] 
            dist[i][j] ← dist[i][k] + dist[k][j]
         end if

Implement this algorithm. The algorithm will need some extensions to allow the reconstruction of the path.

Write three Python functions:

• floyd(adj: str) returns the full calculated matrix.
• floyddist(adj: str, source: int, sink: int) returns the shortest distance between source and sink.
• floydpath(adj: str, source: int, sink: int) returns the shortest path between source and sink. If there are multiple shortest paths, return the path with the fewest nodes.

These functions all receive a string containing an adjacency matrix as input.

Example input

"
- 4 - -
3 - 7 4
- - - 1
5 6 7 -
"

represents an adjacency matrix, corresponding to the weighted adjacency list below:

0:[(4,1)],
1:[(3,0),(7,2),(4,3)],
2:[(1,3)],
3:[(5,0),(6,1),(7,2)]

and corresponding to the graph below:

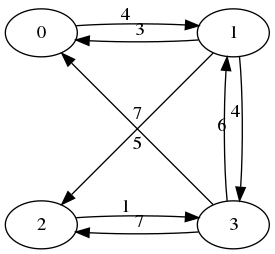
Example

 >>> floyd(open("graaf.in").read())
[[7, 4, 11, 8], [3, 7, 7, 4], [6, 7, 8, 1], [5, 6, 7, 8]]
>>> floyddist(open("graaf.in").read())
8
>>> floydpath(open("graaf.in").read())
[0, 1, 3]

Note:

For all doctests, graaf.in should be in the current directory.