For a slalom competition, the ski slope is divided into a rectangular grid. A number of gates are placed across this grid, each of which is assigned a scores. The rows of the grid are numbered from top to bottom, and the columns from left to right, starting at zero in both cases. This allows us to represent a gate as a tuple $$(r, c, s)$$, where row number $$r$$ and column number $$c$$ indicate where the gate is located, and $$s \in \mathbb{N}_0$$ indicate the gate's score.

A ski slope with a number of gates.

A skier starts at the top (above row 0 of the grid) and can freely choose the position (column) where he starts. With every step the skier always moves

one row down
up to one column to the left or to the right

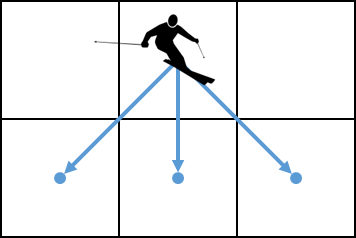
The skier's freedom of movement can therefore be depicted as

De bewegingsvrijheden van een skiër.

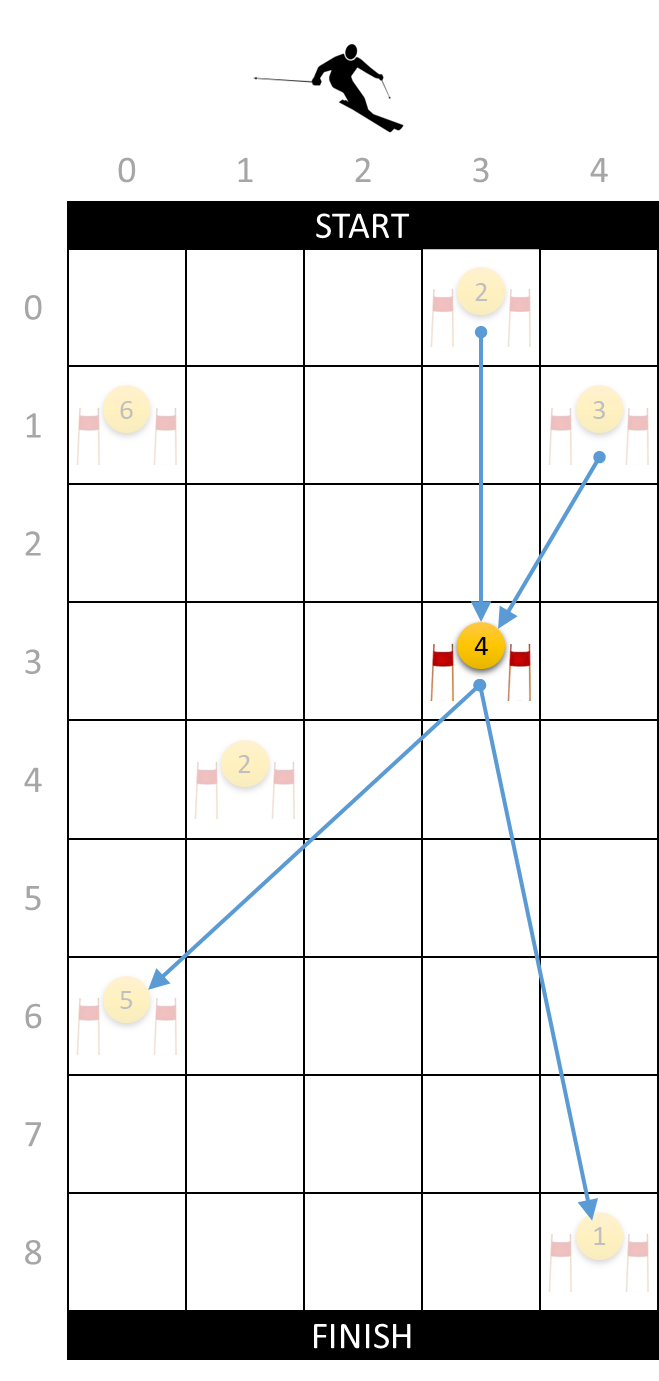
Due to his limited freedom of movement, the skier cannot always follow a course that runs through all the gates on the ski slope. Because he can freely choose his starting position, every gate is reachable from the start, but he cannot necessarily ski from every gate to every other gate. For example, in the left figure below you can see that the gate at position $$(3, 3)$$ is reachable from two higher gates at positions $$(0, 3)$$ and $$(1, 4)$$, and that from this gate only two of the lower gates at positions $$(6, 0)$$ and $$(8, 4)$$ can be reached.

The gate at position $$(3, 3)$$ is reachable from two higher gates at positions $$(0, 3)$$ and $$(1, 4)$$, and from this gate only two of the lower gates at positions $$(6, 0)$$ and $$(8, 4)$$ can be reached.

The course a skier must follow to get the maximal total score of 14.

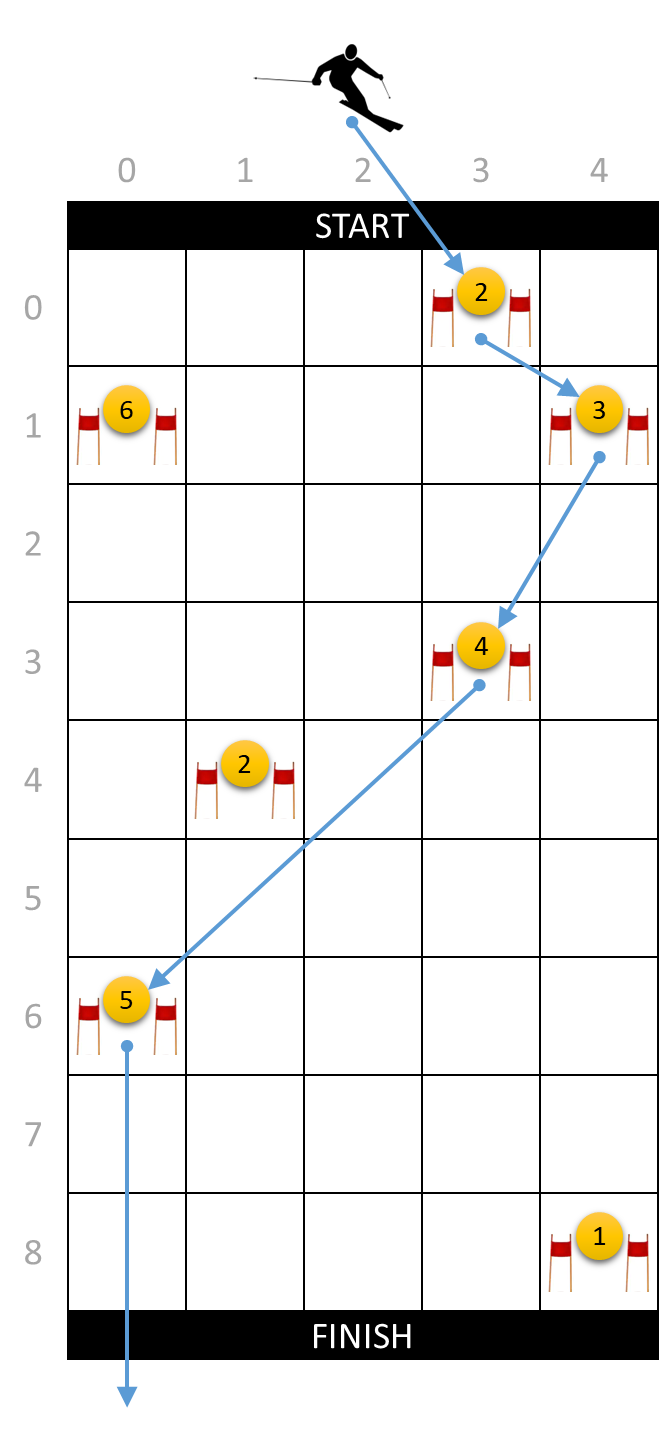
The sum of the scores of all the gates along the course that a skier has followed is called the total score of the course. For a given configuration of a ski slope, we can therefore ask ourselves what maximum total score a skier can get. For the ski slope that we used as an example above, the maximum total score is 14. In the right figure above you see the course the skier must follow to get that total score.

Assignment

The following algorithm can be used to find the maximum total score a skier can get on a given ski slope:

Sort the gates from top to bottom and from left to right: $$p_1, p_2, \ldots, p_n$$
Compute the maximum score at the start and at each gate (in the order determined in step 1).
- The maximum score at the start is equal to zero by definition.
- The maximum score at gate $$p_i$$ is equal to the score of gate $$p_i$$ plus the maximum of the maximum scores at the start and at all previous gates ($$p_1, p_2, \ldots, p_{i-1}$$) from which the gate $$p_i$$ is reachable.
The maximum total score is equal to the maximum of the maximum scores at the start and at all the gates.

Below you can see how this algorithm is applied to the ski slope that we used as an example above.

Toepassing van het algoritme op de voorbeeld skipiste.

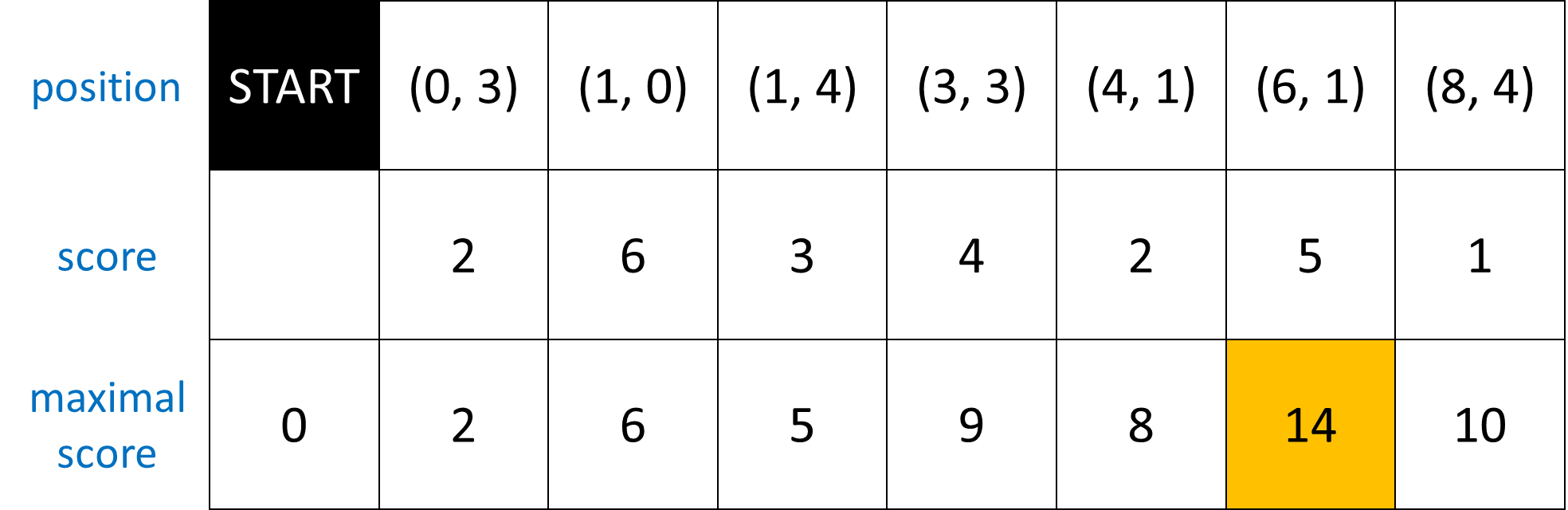
Your task:

Write a function isreachable that takes the positions of two gates $$p$$ and $$q$$. The position of a gate is represented as a tuple $$(r, c)$$, with $$r$$ the number of the row and $$c$$ the number of the column where the gate is located in the grid. The function must return a Boolean value (bool) that indicates if $$p$$ can be reached from $$q$$, or vice versa.
Write a function max_score_gate that can be used to compute the maximum score at a gate (step 2 of the algorithm). The function takes two arguments: i) the gate at which the maximum score must be computed (a tuple $$(r, c, s)$$) and ii) the maximum scores at all previous gates. The second argument is given as a sequence (list or tuple) of tuples $$(r, c, s_{\text{max}})$$ with the row number $$r$$ and the column number $$c$$ of a previous gate, and the maximum score $$s_{\text{max}}$$ at that gate.
Write a function max_total_score that takes a sequence (list or tuple) with the gates on a ski slope. The function must return the maximum total score that a skier can get on the given ski slope.

Example

        >>> isreachable((0, 0), (1, 0))
True
>>> isreachable((0, 5), (2, 1))
False
>>> isreachable((0, 0), (3, 3))
True
>>> isreachable((0, 0), (3, 4))
False

>>> max_score_gate((0, 3, 2), [])
2
>>> max_score_gate((1, 0, 6), [[0, 3, 2]])
6
>>> max_score_gate((1, 4, 3), [[1, 0, 6], [0, 3, 2]])
5
>>> max_score_gate((3, 3, 4), [[1, 4, 5], [0, 3, 2], [1, 0, 6]])
9
>>> max_score_gate((4, 1, 2), [[0, 3, 2], [1, 0, 6], [3, 3, 9], [1, 4, 5]])
8
>>> max_score_gate((6, 1, 5), [[3, 3, 9], [1, 4, 5], [0, 3, 2], [1, 0, 6], [4, 1, 8]])
14
>>> max_score_gate((8, 4, 1), [[6, 1, 14], [4, 1, 8], [1, 0, 6], [1, 4, 5], [3, 3, 9], [0, 3, 2]])
10

>>> max_total_score([(0, 3, 2), (1, 4, 4), (3, 2, 2), (5, 4, 4), (8, 4, 3)])
15
>>> max_total_score([(0, 1, 1), (2, 0, 2), (3, 2, 4)])
5