Piet Mondrian was a Dutch painter and considered one of the great artists of the 20th century. Some of Mondrian's artwork has a unique, geometric style.

In a Mondrian art puzzle, you have to tile a square $$n \times n$$ grid ($$n$$ rows and $$n$$ columns) with non-overlapping rectangles that each cover a number of grid cells.

The dimensions of an $$h \times w$$ rectangle are described by two integers: the number of rows $$h$$ and the number of columns $$w$$ of the grid covered by the rectangle. The area of an $$h \times w$$ rectangle is equal to the number of squares covered: $$h \times w$$. It is not allowed to use two rectangles of the same dimensions: if you cover part of the grid with an $$h \times w$$ rectangle, the tiling may not use any other $$h \times w$$ or $$w \times h$$ rectangles. However, a tiling may have two rectangles of the same area.

The score of a tiling is equal to the area of the largest rectangle minus the area of the smallest rectangle. The goal is to find a tiling with the smallest possible score.

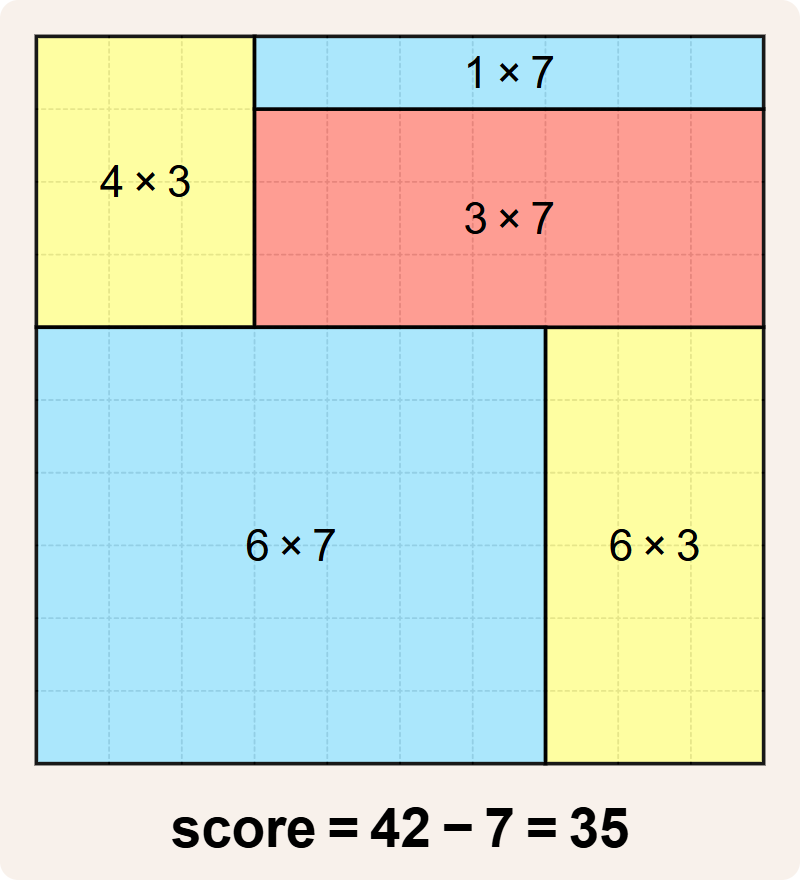
For example, this tiling covering a $$10 \times 10$$ grid has score $$42 - 7 = 35$$.

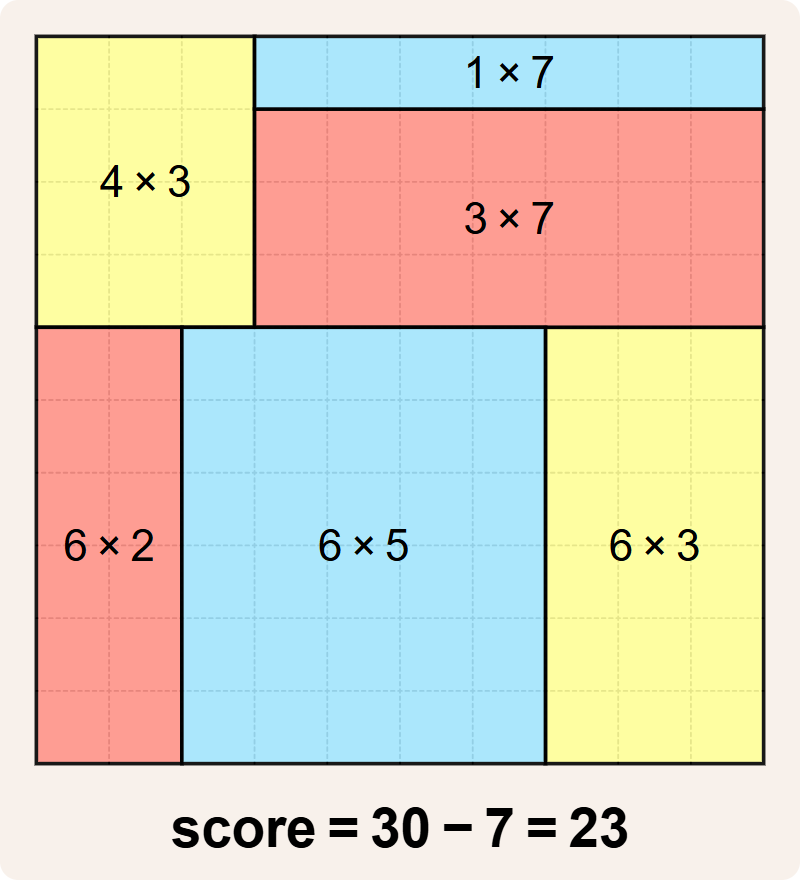
Better tilings are possible. For example, here's a tiling with score $$30 - 7 = 23$$. Still suboptimal, but much better than what we had before.

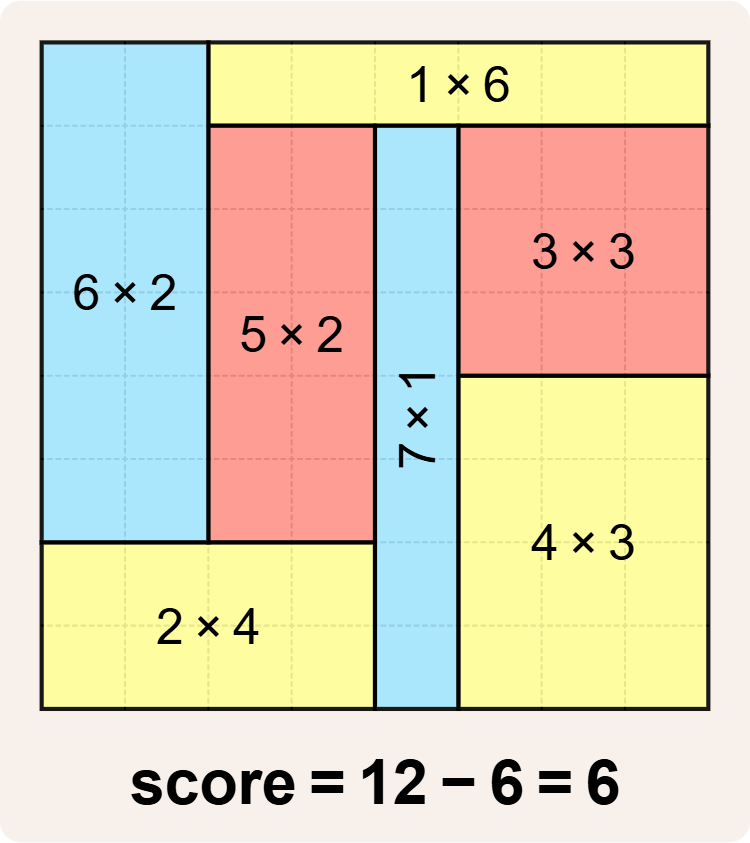
Note that although the $$4 \times 3$$ rectangle and the $$6 \times 2$$ rectangle have the same area ($$12$$), this is a valid tiling because the rectangles have different dimensions. However, there is an even better tiling with score $$25 - 7 = 18$$.

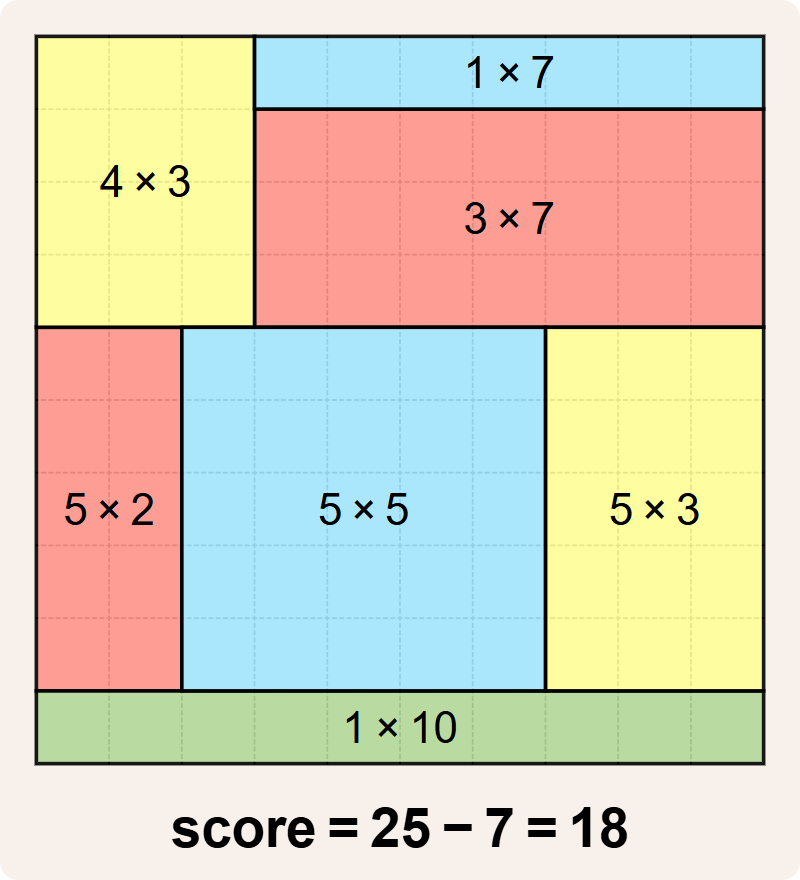
The tiling below might look like the best one we have found so far, but it is not. It violates the rule that tilings cannot have rectangles of the same dimensions. This tiling has a $$4 \times 3$$ rectangle and a $$3 \times 4$$ rectangle, and that's not allowed. The $$5 \times 2$$ rectangle and the $$1 \times 10$$ rectangle have the same area ($$10$$), but because they have different dimensions, they can co-habit the same tiling.

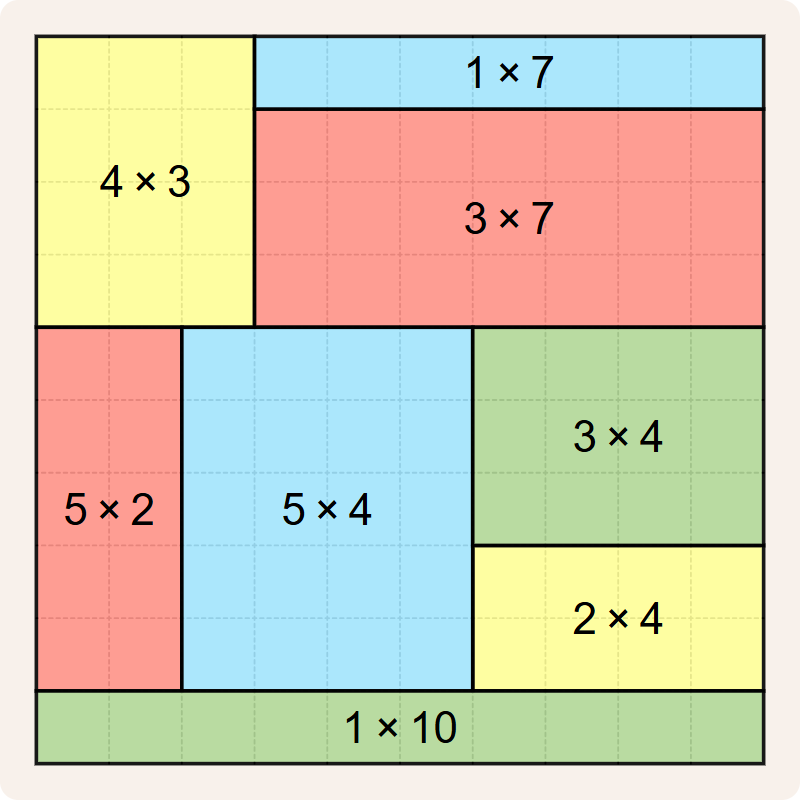
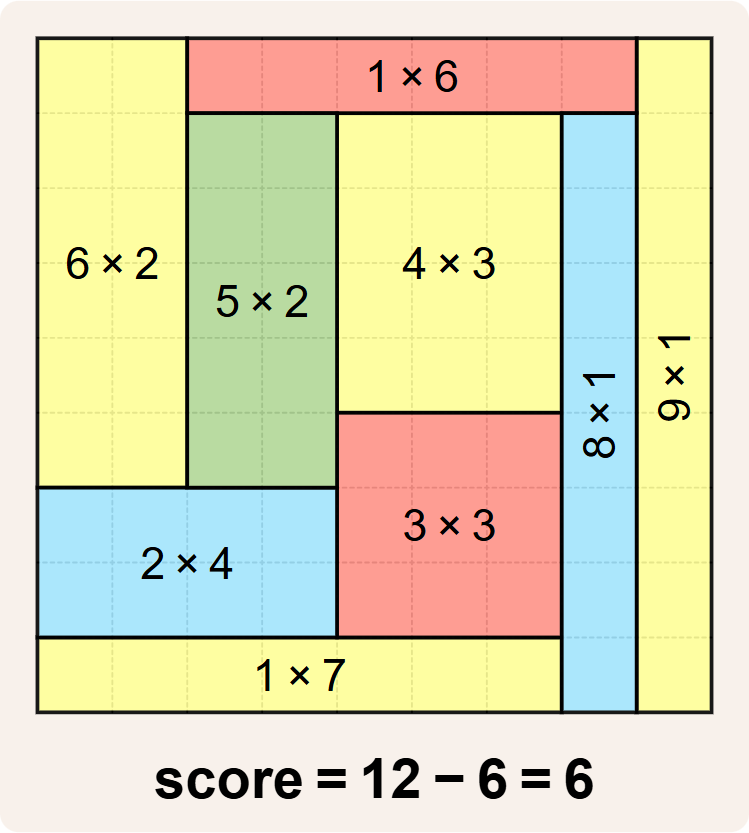
As a bonus, we colored all rectangles using the fewest number of colors possible so that no two rectangles of the same color touch along an edge or a vertex.

Assignment

Define a class Mondrian that allows tiling square $$n \times n$$ grids ($$n$$ rows and $$n$$ columns) according to the rules of a Mondrian art puzzle. The grid dimension $$n$$ (int) must be passed when creating a new tiling (Mondrian).

To locate grid cells, we number the rows of the grid from top to bottom and the columns from left to right, each time starting from zero. As such, we can represent the position of a cell as a tuple $$(r, c)$$, with $$r$$ the number of the row ($$0 \leq r < n$$) and $$c$$ the number of the column ($$0 \leq c < n$$) containing the cell.

It should be possible to add rectangles to and remove rectangles from a tiling. When adding a rectangle, it is indicated by the first unused capital of the alphabet. A tiling $$\mathcal{M}$$ (Mondriaan) must support at least the following methods:

• A method next_letter that takes no arguments. The method must return the first capital (str) in the alphabet that does not indicate a rectangle in tiling $$\mathcal{M}$$.

• A method cells that takes four arguments: i) a row number $$r$$ (int; parameter row), ii) a column number $$c$$ (int; parameter col), iii) a height $$h$$ (int; parameter height), and iv) a width $$w$$ (int; parameter width). These arguments describe an $$h \times w$$ rectangle whose upper left corner would cover the cell on row $$r$$ and column $$c$$ in the grid of tiling $$\mathcal{M}$$. If the rectangle is not completely inside the grid of tiling $$\mathcal{M}$$, an AssertionError must be raised with message invalid rectangle. Otherwise, the method must return a set containing the positions (tuple) of all cells in the grid of tiling $$\mathcal{M}$$ that would be covered by the rectangle.

• A method add_rectangle that takes four arguments: i) a row number $$r$$ (int; parameter row), ii) a column number $$c$$ (int; parameter col), iii) a height $$h$$ (int; parameter height), and iv) a width $$w$$ (int; parameter width). These arguments describe an $$h \times w$$ rectangle whose upper left corner covers the cell on row $$r$$ and column $$c$$ in the grid of tiling $$\mathcal{M}$$. This rectangle must satisfy the following conditions:

  1. the rectangle is completely inside the grid of tiling $$\mathcal{M}$$

  2. tiling $$\mathcal{M}$$ has no other rectangle with the same dimensions (no $$h \times w$$ rectangle and no $$w \times h$$ rectangle)

  3. the rectangle does not overlap with another rectangle in tiling $$\mathcal{M}$$

  If at least one of these conditions is violated, an AssertionError must be raised with message invalid rectangle and no rectangle should be added to tiling $$\mathcal{M}$$. Otherwise, the rectangle must be added to tiling $$\mathcal{M}$$ (indicated by the first capital in the alphabet that is not already assigned to another rectangle in tiling $$\mathcal{M}$$) and the method must return a reference to tiling $$\mathcal{M}$$.

• A method remove_rectangle that takes a capital $$R$$ (str). If capital $$R$$ does not indicate a rectangle in tiling $$\mathcal{M}$$, an AssertionError must be raised with message invalid rectangle and no rectangle should be removed from tiling $$\mathcal{M}$$. Otherwise, the rectangle indicated by capital $$R$$ must be removed from tiling $$\mathcal{M}$$, and the method must return a reference to tiling $$\mathcal{M}$$. In removing a rectangle from tiling $$\mathcal{M}$$, the capital indicating the rectangle is released and can be reused to indicate a new rectangle added to tiling $$\mathcal{M}$$ afterwards.

• A method coverage that takes no arguments. The method must return the coverage (int) of tiling $$\mathcal{M}$$: the number of grid cells covered by the rectangle.

• A method score that takes no arguments. The method must return the score (int) of tiling $$\mathcal{M}$$. If tiling $$\mathcal{M}$$ does not cover all grid cells, the score is -1 by definition.

If a tiling $$\mathcal{M}$$ (Mondrian) is passed to the built-in function str, a string representation (str) of the grid of tiling $$\mathcal{M}$$ must be returned. Each row of the grid is represented as a separate line, and each cell is represented by the capital indicating the rectangle covering the cell in tiling $$\mathcal{M}$$, or an underscore (_) if the cell is not covered by a rectangle in tiling $$\mathcal{M}$$.

Example

In the following interactive session, we use the optimal tiling of a $$10 \times 10$$ grid with score 18 from the introduction as an example to illustrate how the class Mondrian must behave.

>>> puzzle = Mondrian(10)
>>> print(puzzle)
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
>>> puzzle.coverage()
0
>>> puzzle.score()
-1
>>> puzzle.next_letter()
'A'
>>> puzzle.cells(row=4, col=0, height=5, width=2) # doctest: +SKIP
{(4, 0), (4, 1), (5, 0), (5, 1), (6, 0), (6, 1), (7, 0), (7, 1), (8, 0), (8, 1)}
>>> print(puzzle.add_rectangle(row=4, col=0, height=5, width=2))
__________
__________
__________
__________
AA________
AA________
AA________
AA________
AA________
__________
>>> puzzle.coverage()
10
>>> puzzle.score()
-1
>>> puzzle.next_letter()
'B'
>>> puzzle.cells(row=1, col=3, height=3, width=7) # doctest: +SKIP
{(1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9), (2, 3), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (2, 9), (3, 3), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (3, 9)}
>>> print(puzzle.add_rectangle(row=1, col=3, height=3, width=7))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA________
AA________
AA________
__________
>>> puzzle.cells(row=8, col=8, height=3, width=3)           # rectangle not enclosed within square
Traceback (most recent call last):
AssertionError: invalid rectangle
>>> puzzle.add_rectangle(row=8, col=8, height=3, width=3)   # rectangle not enclosed within square
Traceback (most recent call last):
AssertionError: invalid rectangle
>>> puzzle.add_rectangle(row=5, col=4, height=2, width=5)   # other rectangle has same dimensions
Traceback (most recent call last):
AssertionError: invalid rectangle
>>> puzzle.add_rectangle(row=2, col=1, height=3, width=3)   # rectangle overlaps with other rectangle
Traceback (most recent call last):
AssertionError: invalid rectangle
>>> print(puzzle)
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA________
AA________
AA________
__________
>>> puzzle.next_letter()
'C'
>>> print(puzzle.add_rectangle(row=6, col=7, height=3, width=3))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA_____CCC
AA_____CCC
AA_____CCC
__________
>>> puzzle.next_letter()
'D'
>>> print(puzzle.add_rectangle(row=9, col=0, height=1, width=10))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA_____CCC
AA_____CCC
AA_____CCC
DDDDDDDDDD
>>> puzzle.remove_rectangle('X')
Traceback (most recent call last):
AssertionError: invalid rectangle
>>> puzzle.next_letter()
'E'
>>> print(puzzle.remove_rectangle('C'))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA________
AA________
AA________
DDDDDDDDDD
>>> puzzle.next_letter()
'C'
>>> print(puzzle.add_rectangle(row=0, col=0, height=4, width=3))
CCC_______
CCCBBBBBBB
CCCBBBBBBB
CCCBBBBBBB
AA________
AA________
AA________
AA________
AA________
DDDDDDDDDD
>>> puzzle.coverage()
53
>>> puzzle.score()
-1
>>> print(puzzle.add_rectangle(0, 3, 1, 7).add_rectangle(4, 7, 5, 3).add_rectangle(4, 2, 5, 5))
CCCEEEEEEE
CCCBBBBBBB
CCCBBBBBBB
CCCBBBBBBB
AAGGGGGFFF
AAGGGGGFFF
AAGGGGGFFF
AAGGGGGFFF
AAGGGGGFFF
DDDDDDDDDD
>>> puzzle.coverage()
100
>>> puzzle.score()
18

The solutions you submit are also tested using these tilings.