DNA consists of four different bases, represented by the uppercase letters A, C, G and T. These bases have a specific meaning within our biology: withing the coding part of a gene, a triplet of bases encodes for an amino acid.
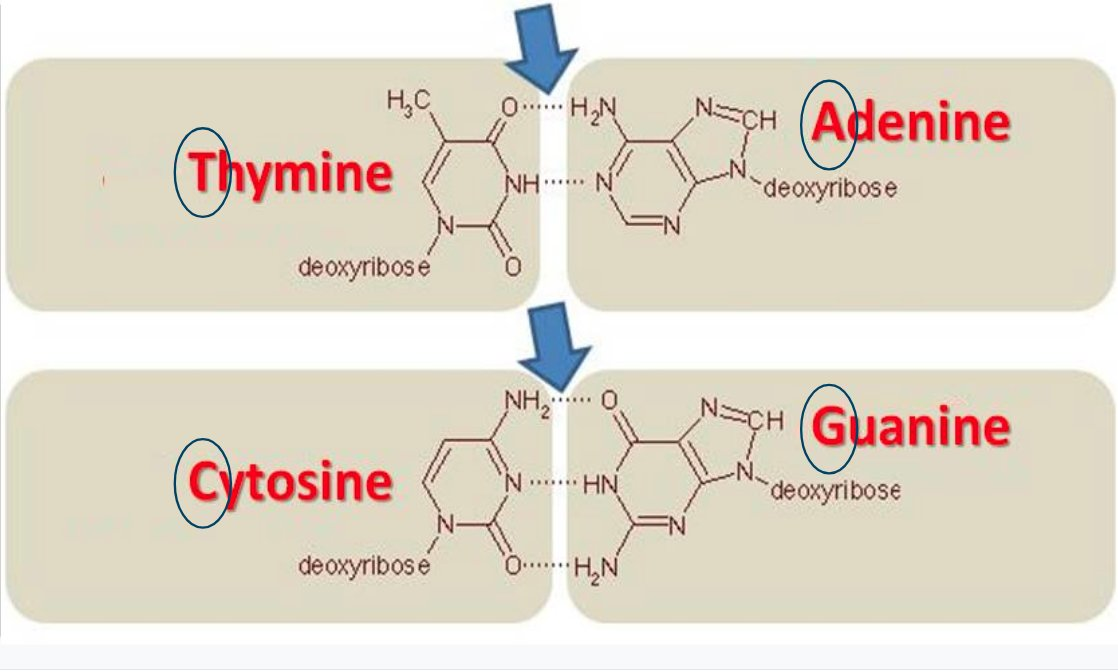
Most DNA is stored redundantly in two connected strands. Wherever there is an A on one strand, you'll find a T on the other strand (and vice versa). Similarly, C and G are also complementary to each other.
T G T C A G T A C A G T C A
Note how the letters of one of the two strands are usually drawn upside down: this matters! After all, one strand is read from left to right, and the other from right to left. If we have one strand of DNA, the other strand is obtained as its reverse complement1 by inverting the DNA strand and then replacing each base with its complement (A by T and vice versa, and C by G and vice versa).

If you take all the DNA of an organism (both strands), you will find equal numbers of A's and T's, as well as equal number of C's and G's. This is true by definition due to the complementarity of the bases on opposites sides of both strands, and it is called Chargaff's first parity rule2.

Strangely enough, this rule also applies to a single DNA strand. So even if you take away the redundancy, you still get about equal numbers of A/T and G/C per DNA strand. This is called Chargaff's second parity rule3.
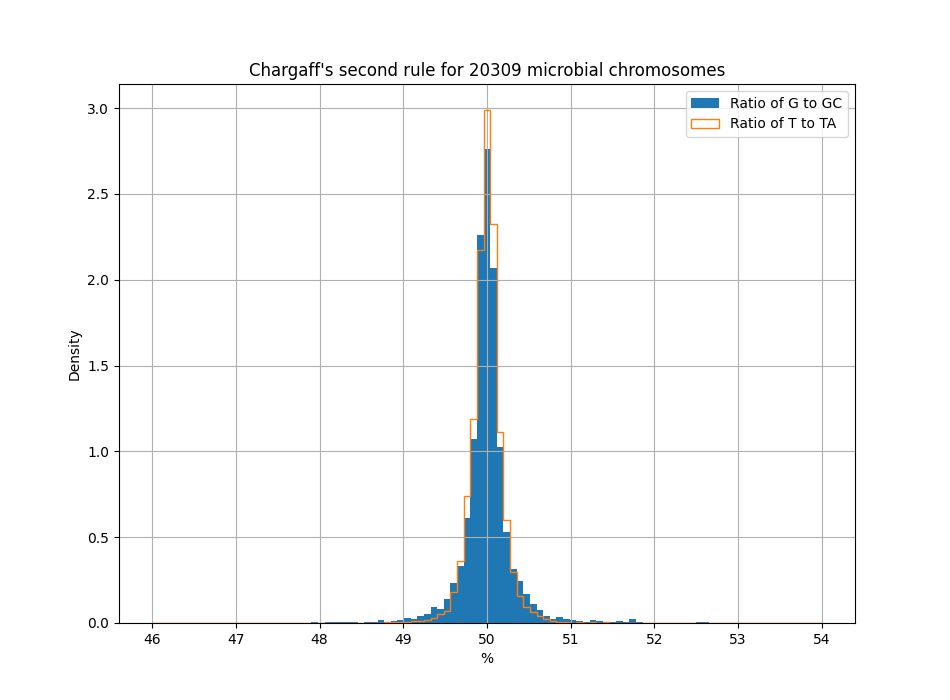
Scientists have put forward several theories to explain why the number of complementary bases should match up on a single DNA strand — one more advanced than the other4 — but as yet no slam dunk explanation have been reported. But, hold on, things are about to get even weirder.
It turns out the rule also holds for so-called $$k$$-mers, as long as we compare the occurrences of a $$k$$-mer with its reverse complement. A $$k$$-mer is nothing but $$k$$ consecutive bases in a DNA strand. For $$k > 1$$, successive $$k$$-mers overlap. For example, a DNA strand ACGCTAG has six 2-mers (AC, CG, GC, CT, TA and AG) and five 3-mer (ACG, CGC, GCT, CTA and TAG). So for $$k=1$$, the rule says that the number of C's and G's is about the same. For $$k=2$$ there are, for example, about as many CC's as there are GG's, about as many AG's as there are CT's (reverse complement), and so on.
For DNA triplets ($$k=3$$) such as AAA the analysis may yield results as in the graph below. In this graph we put the number of occurrences of two complementary triplets next to each other. On the left is a blue bar indicating, for example, the number of occurrences of AAA, and on the right an orange bar indicating the number of occurrences of the reverse complement TTT. We do this for the 32 triplet pairs. The correspondence between the number of occurrences for each pair is stunning:
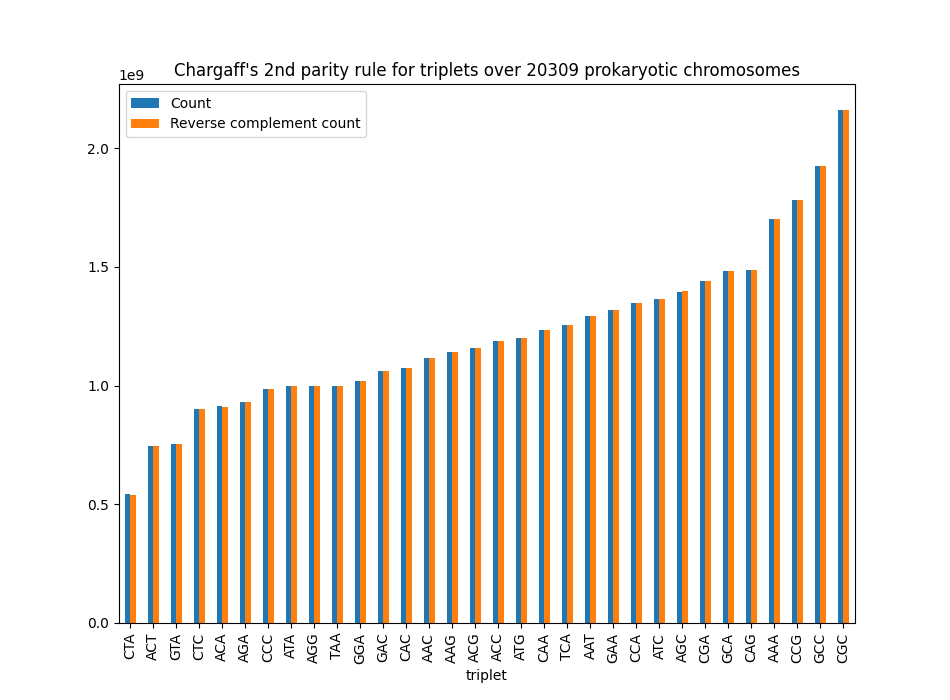
So again, why is this the case? There are lots and lots of theories, but there is no consensus yet. And that is what makes it so super interesting! At the very core of life hides a mystery that we can easily analyze using a computer. This way, we hope that we can unravel the mystery one day soon.
Assignment
We ask you to define a class DNA to represent DNA strands, a function read_fasta to read a DNA strand from a FASTA file, and a class Analysis to perform $$k$$-mer analyses on a DNA strand.
DNA strands
Define a class DNA to represent DNA strands. When creating a new DNA strand (DNA), a string (str) must be passed with the consecutive bases of the DNA strand. If the string contains a character that is no A, C, G or T, an AssertionError must be raised with the message invalid DNA strand. DNA strands (DNA) are immutable.
-
If a DNA strand (DNA) is passed to the built-in function len, the length of the DNA strand must be returned. This is a number (int) that indicates how many bases occur in the DNA strand.
-
If a DNA strand (DNA) is passed to the built-in function repr, a string representation (str) must be returned that reads as a Python expression to create a new DNA strand (DNA) with the same bases as the DNA strand passed to the function repr.
-
If a DNA strand (DNA) is passed to the built-in function str, a string (str) must be returned with the representation of the successive bases of the DNA strand.
-
For two DNA strands $$s_1$$ and $$s_2$$ (DNA), the expression $$s_1 + s_2$$ must yield a new DNA strand (DNA) with the bases of $$s_1$$ followed by the bases of $$s_2$$.
-
DNA strands must also have a method reverse_complement that takes no arguments. The method must return a new DNA strand (DNA) whose bases are the reverse complement of the DNA strand on which the method is called.
FASTA files
Define a function read_fasta that takes the location (str) of a FASTA file. The function must return the DNA strand (DNA) from the file.
A FASTA file is a text file that stores a DNA strand. The first line of the file starts with a greater than symbol (>), followed by a free-text description of the DNA strand. This is followed by one or more lines containing the successive bases of the DNA strand. For example, this file (seq.fasta5) contains a DNA strand with 42 bases.
>seq AGCTGCATGACTACGACTAC TAGTCGGATTAGGCATGCTA CT
$$k$$-mer analyses
Define a class Analysis to perform $$k$$-mer analyses on a DNA strand. When creating a $$k$$-mer analysis (Analysis), two arguments must be passed: i) a DNA strand $$\delta$$ (DNA) and ii) a number $$k \in \mathbb{N}_0$$ (int). A $$k$$-mer analysis (Analysis) must support at least the following methods:
-
A method kmers that takes no arguments. The method must return a list containing the successive $$k$$-mers in DNA strand $$\delta$$, where the $$k$$-mers are represented as strings (str).
-
A method count that takes a string $$\kappa$$ (str). If $$\kappa$$ does not contain $$k$$ letters or if at least one of the letters does not represent a DNA base (A, C, G or T), an AssertionError must be raised with the message invalid k-mer. Otherwise the method must return a tuple with two numbers (int): i) the number of occurrences of $$k$$-mer $$\kappa$$ in DNA strand $$\delta$$ and ii) the number of occurrences of the reverse complement of $$k$$-mer $$\kappa$$ in DNA strand $$\delta$$.
Example
The following interactive sessions assumes the FASTA files seq.fasta6 and mitochondrion.fasta7 are located in the current directory.
>>> dna1 = DNA('AGCTTTTCATTCTGACTGCATGATAGCAGC')
>>> dna1
DNA('AGCTTTTCATTCTGACTGCATGATAGCAGC')
>>> print(dna1)
AGCTTTTCATTCTGACTGCATGATAGCAGC
>>> len(dna1)
30
>>> dna1.reverse_complement()
DNA('GCTGCTATCATGCAGTCAGAATGAAAAGCT')
>>> DNA('XYZ')
Traceback (most recent call last):
AssertionError: invalid DNA strand
>>> dna2 = read_fasta('seq.fasta8')
>>> dna2
DNA('AGCTGCATGACTACGACTACTAGTCGGATTAGGCATGCTACT')
>>> len(dna2)
42
>>> dna2.reverse_complement()
DNA('AGTAGCATGCCTAATCCGACTAGTAGTCGTAGTCATGCAGCT')
>>> dna3 = dna1 + dna2
>>> dna3
DNA('AGCTTTTCATTCTGACTGCATGATAGCAGCAGCTGCATGACTACGACTACTAGTCGGATTAGGCATGCTACT')
>>> len(dna3)
72
>>> analysis = Analysis(dna1, 2)
>>> analysis.kmers()
['AG', 'GC', 'CT', 'TT', 'TT', 'TT', 'TC', 'CA', 'AT', 'TT', 'TC', 'CT', 'TG', 'GA', 'AC', 'CT', 'TG', 'GC', 'CA', 'AT', 'TG', 'GA', 'AT', 'TA', 'AG', 'GC', 'CA', 'AG', 'GC']
>>> analysis.count('TT')
(4, 0)
>>> analysis.count('GA')
(2, 2)
>>> analysis.count('ACT')
Traceback (most recent call last):
AssertionError: invalid k-mer
>>> mitochondrion = read_fasta('mitochondrion.fasta9')
>>> len(mitochondrion)
16569
>>> analysis = Analysis(mitochondrion, 3)
>>> analysis.count('TT')
Traceback (most recent call last):
AssertionError: invalid k-mer
>>> analysis.count('GTA')
(154, 377)
>>> analysis.count('CTG')
(180, 199)