A chessboard is the type of checkerboard used in the classic board game chess, and consists of 64 squares. The squares are arranged in a grid with eight rows and eight columns, having two alternating colors: light and dark. The columns of a chessboard are labeled from left to right by the letters a–h, the rows from bottom to top by the numbers 1–8. This way, the position of each square on the chessboard is identified by the letter of the column and the number of the row where the square can be found in the grid.
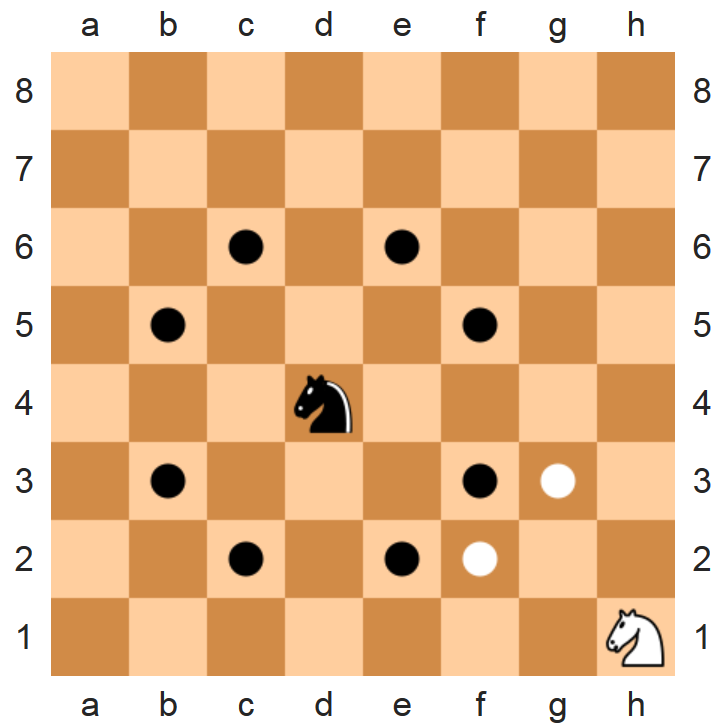
The knight is one of six different pieces in the game of chess. It is normally represented by a horse's head and neck. The way the knight moves across the chessboard — the knight move — is unusual among chess pieces. It may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically. The complete move therefore forms the shape of the letter L, and moves the knight alternately to light and dark squares.
While moving, the knight can jump over pieces (of either color) to reach its destination. Knights capture in the same way, replacing the enemy piece on the square and removing it from the board. Knights and bishops, also known as minor pieces, are considered approximately equal in value. Bishops utilize a longer range, but can only move to squares of one color. The knight's value increases in closed positions since it can jump over blockades. Knights and bishops are stronger when supported by other pieces (such as pawns) to create outposts and become more powerful when they advance, as long as they remain active.
The knight, along with the king and the rook, has the oldest defined movement of any chess piece, its movement being unchanged since the invention of chaturanga1 in India around the 6th century. Similar pieces are found in almost all games of the chess family.
Input
Two lines that each identify the position of a square on the chessboard.
Output
A line indicating if a knight can jump from the first square to the second square on a chessboard. Take a look at the examples below to see how the output must be formatted.
Example
Input:
d4
e6Output:
a knight can jump from d4 to e6Example
Input:
h1 c2
Output:
a knight cannot jump from h1 to c2
Epilogue
The Lo Shu square2 is the $$3 \times 3$$ square enclosed in dashed lines at the center of the diagram below. It's "magic": each row, column, and long diagonal (marked in red) sums to 15.
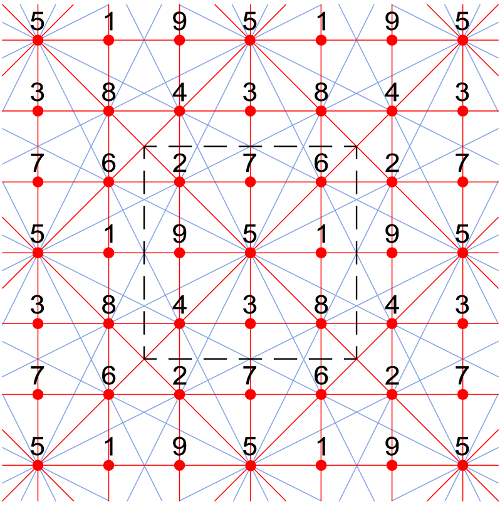
William Walkington has discovered a new magic property3. Imagine rolling the square into a tube (in either direction), and then bending the tube into a torus4. And now imagine hopping from cell to cell around the torus with a knight's move — two cells over and one up. The extended diagram above helps with visualizing this — follow the blue lines. It turns out that each such path touches three cells, and these cells always sum to 15. So the square is even more magic than we thought.