Forget about sudoku puzzles. The latest craze in logic puzzles is hidato. Today hidato is featured in over 60 newspapers around the world. At any moment, thousands of people play hidato online. Hidato's slogan "Find the Path… Solve the Puzzle!" is now well-known among scores of puzzle-solvers and it will probably bring fun and teach logic skills to many more in the near future. The term hidato originates from the Hebrew word for riddle (Hida, חידאתו) and is the name of a logic puzzle game invented by Dr. Gyora Benedek, an Israeli computer scientist, inventor and adventurer.
A hidato consists of a rectangular grid with $$m$$ rows and $$n$$ columns. The goal is to fill the grid with the series of consecutive numbers 1 to $$m \times n$$ adjacent to each other vertically, horizontally, or diagonally. In every hidato the positions of the numbers 1 and $$m \times n$$ on the grid are given. There are also other given numbers on the grid (with values between 1 and $$m \times n$$) to help direct the player how to start the solution and to ensure the hidato has a unique solution.
Assignment
In this assignment, we represent a $$m \times n$$ grid containing the solution of a hidato as a list containing $$m$$ elements. These elements represent the rows of the grid. Each row is itself a list containing $$n$$ integers. These represent the numbers which are filled in the successive columns of the row. You may assume that each of the numbers 1, 2, …, $$m \times n$$ occurs just once in the grid. The rows of the grid are indexed from top to bottom, and the columns from left to right. Indexing of the rows and columns always starts from 0. Your task is to determine whether a given $$m \times n$$ grid represents a valid solution of a hidato. In order to do so, you proceed as follows:
-
Write a function first that takes the solution of a hidato as its argument. The function must return a tuple (r, c) that contains the row index r and the column index c of the cell in the grid that contains the value 1.
-
Write a function successor that takes three arguments. The first argument is the solution of a hidato. The second and third arguments respectively represent the row and column index of a cell in the grid. The function must return a tuple (r, c) that contains the row index r and the column index c of the cell in the grid that follows upon the given cell. If the given cell contains the integer $$v$$, its successor is the vertically, horizontally, or diagonally adjacent cell that contains the value $$v + 1$$. If the given cell has no successor, the function should return the tuple (None, None).
-
Use the functions first and successor to write a function last that takes the solution of a hidato as its argument. The function must return a tuple (r, c) that contains the row index r and the column index c of the cell in the grid that is found by starting from the cell containing the value 1, and repetitively visiting the next cell until a cell is reached that has no successor. The coordinates of the last visited cell must be return by the function.
-
Use the function last to write a function hidato that takes the solution of a hidato as its argument. The function must return a Boolean value that indicates whether or not the given grid is a valid solution of a hidato. This can be determined by starting from the cell containing the value 1, and repetitively visiting the next cell until a cell is reached that has no successor. In case the last visited cell contains an integer that is equal to the total number of cells in the grid, the given grid represents a valid solution of a hidato.
Example
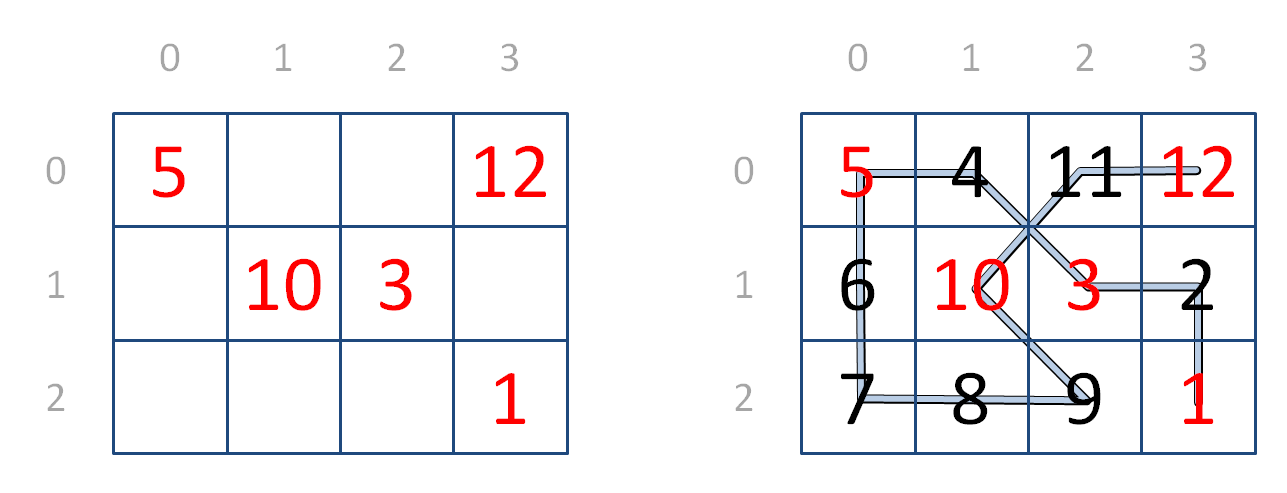
>>> first([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]])
(2, 3)
>>> first([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]])
(1, 1)
>>> first(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10)))
(1, 1)
>>> successor([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]], 2, 3)
(1, 3)
>>> successor([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]], 1, 3)
(1, 2)
>>> successor([[5, 4, 11, 2], [6, 10, 3, 12], [7, 8, 9, 1]], 2, 3)
(None, None)
>>> last([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]])
(0, 3)
>>> last([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]])
(3, 2)
>>> last(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10)))
(0, 2)
>>> hidato([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]])
True
>>> hidato([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]])
False
>>> hidato(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10)))
TrueFun Fact
When asked by The New York Times where he got the idea for hidato, Dr. Benedek gave the following anwser
During SCUBA diving, I noticed a school of fish swimming at amazing speed around me. They were so fast that I could only see them at the spots where they changed direction. In my mind I worked hard to reconstruct their path. I was so fascinated that I hadn't noticed the time and the level of oxygen in my tank. Luckily, my partner signaled — time to surface. I was reluctant to leave behind this amazing dance of fish and it was still in my mind when I noticed a crumpled and wet newspaper in the shower. The only dry spot in the paper was a Sudoku puzzle. And then an idea popped in my mind: How about a printed puzzle where you reconstruct the path of the fish from observed spots? I couldn't wait to get home and start building the puzzle. A couple of weeks later, I knew I had something big. This is how Hidato was born.