Valknut is a cipher in which each symbol (a letter, a number, a punctuation mark or a space) is represented as a unique combination of two digits (1–9). Conversely, each digit pair (1–9) corresponds to a unique symbol. Because the digit zero is not used, there are 81 different digit pairs in total, and therefore also 81 different symbols.

A key for the valknut-cipher specifies which digit pair $$ij$$ ($$1 \leq i, j \leq 9$$) corresponds with each symbol $$\alpha$$ (a letter, a digit, a punctuation mark or a space). This is done in a text file that contains 81 lines. Each line contains one symbol $$\alpha$$, followed by the corresponding digit $$i$$ and the corresponding digit $$j$$, each separated by a tab. Note that a tab is never used as a symbol in the valknut-cipher. Such a file could for example look like this (valknut.txt¹):

W	2	6
?	9	5
 	6	8
h	3	8
(	4	8
e	6	3
4	8	6
z	7	6
.	2	7
P	5	8
!	9	9
d	8	9
⋮	⋮	⋮

According to this key, capital W is represented as digit pair 26, lowercase e as digit pair 63, digit 4 as digit pair 86, a space as digit pair 68, and a dot (.) as digit pair 27.

To quickly look up the symbol $$\alpha$$ that corresponds with a digit pair $$ij$$ ($$1 \leq i, j \leq 9$$), the 81 symbols of a valknut-key are placed in a $$9 \times 9$$ grid with 9 rows and 9 columns. The rows of the grid are numbered from top to bottom, and the columns from left to right, each starting from 1. The digit pair $$ij$$ is then nothing but the row number $$i$$ and the column number $$j$$ of the cell in the grid where the corresponding symbol $$\alpha$$ can be found. This is the grid for our example key:

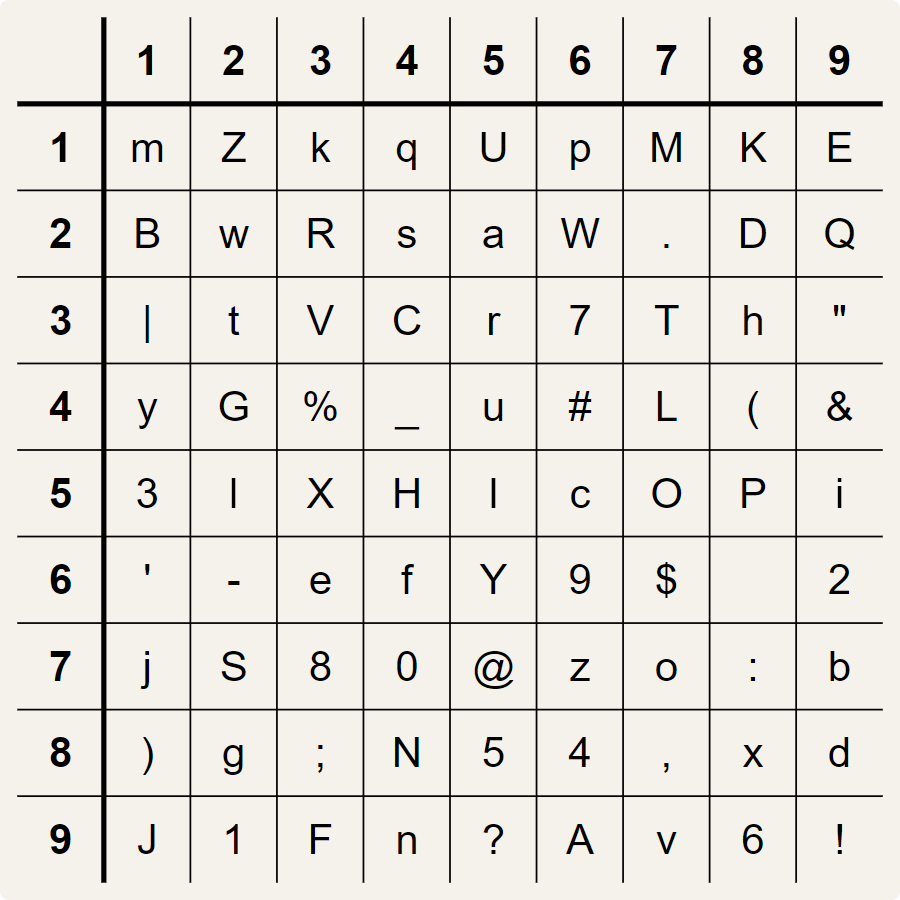
For digit pair 26 we find capital W in this grid on row 2 and column 6. Analogously, digit pair 63 corresponds to lowercase e, digit pair 86 to digit 4, digit pair 68 to a space (empty cell on row 6 and column 8), and digit pair 27 to a dot (.).

Encode and decode

Vikings are best known as formidable warriors who excelled in physical strength. However, they were also extremely intelligent and spiritually inclined. This is one of their important life lessons:

Where wolf's ears are, wolf's teeth are near.

We use our example key from the introduction (valknut.txt²) to illustrate how this plaintext is encoded according to the valknut-cipher. First, we convert each symbol of the plaintext into its corresponding digit pair (W→  26, h → 38, e → 63, …, . → 27). Chaining all these digit pairs together, we get the following digit sequence:

263863356368227752646124686325352468253563876822775264612468326363323868253563689463253527

If we would convert each digit pair of this sequence into its corresponding symbol, we would obviously get back to the original plaintext. But we first swap the order of the two digits of each digit pair. This yields the following digit sequence:

628336533686227725461642863652534286525336788622772546164286233636238386525336864936525372

If we now convert each digit pair of this sequence back into its corresponding symbol, we get the following ciphertext:

-;7X74woa#pG47lXG4lX7:4woa#pG4R77R;4lX74&7lXS

It is very easy to decode this ciphertext, as the procedure works in exactly the same way as encoding the plaintext.

Assignment

• Write a function read_key that takes the location (str) of a text file specifying a valknut-key $$\mathcal{V}$$. The function must return the dictionary representation of valknut-key $$\mathcal{V}$$: a dictionary (dict) that maps each symbol $$\alpha$$ (str) of the key onto a tuple $$(i, j)$$, where $$i$$ (int) and $$j$$ (int) together form the digit pair $$ij$$ ($$1 \leq i, j \leq 9$$) that corresponds to symbol $$\alpha$$ according to the key.

• Write a function symbols2digits that takes two arguments: i) a sequence of symbols $$s$$ (str) and ii) the dictionary representation (dict) of a valknut-key $$\mathcal{V}$$. The function may assume that all symbols in $$s$$ occur in key $$\mathcal{V}$$, without having to check this explicitly. The function must return the digit sequence $$c$$ (str) that corresponds to sequence $$s$$ according to key $$\mathcal{V}$$. The function also has a third optional swap that may take a Boolean value (bool; default value: False). If the parameter swap takes the value True, then each digit pair must be swapped in the sequence $$c$$ returned by the function.

• Write a function make_grid that takes the dictionary representation (dict) of a valknut-key $$\mathcal{V}$$. The function must return the grid representation of valknut-key $$\mathcal{V}$$: a new dictionary (dict) that maps each digit 1–9 (int) onto a string (str) containing the symbols on the corresponding row in the grid representation of the key (listed from left to right).

• Write a function digits2symbols that takes two arguments: i) a digit sequence $$c$$ (str) and ii) the grid representation of a valknut-key $$\mathcal{V}$$. The function may assume that sequence $$c$$ consists of an even number of digits 1–9, without having to check this explicitly. The function must return the sequence of symbols $$s$$ (str) that corresponds to sequence $$c$$ according to key $$\mathcal{V}$$. The function also has a third optional parameter swap that may take a Boolean value (bool; default value: False). If the parameter swap takes the value True, then each digit pair must be swapped in sequence $$c$$ before the function determines the corresponding symbols for sequence $$s$$.

• Write a function encode that takes two arguments: i) a plaintext $$t$$ (str) and ii) the dictionary representation (dict) of a valknut-key $$\mathcal{V}$$. The function must return the ciphertext (str) obtained upon encoding plaintext $$t$$ according to the valknut-cipher with key $$\mathcal{V}$$.

• Write a function decode that takes two arguments: i) a ciphertext (str) obtained upon encoding a plaintext $$t$$ according to the valknut-cipher and ii) the dictionary representation (dict) of the valknut-key $$\mathcal{V}$$ that was used for encoding. The function must return plaintext $$t$$.

Example

In the following interactive session, we assume the text file valknut.txt³ is located in the current directory.

>>> key = read_key('valknut.txt4')
>>> key['W']
(2, 6)
>>> key['h']
(3, 8)
>>> key[' ']
(6, 8)
>>> key['.']
(2, 7)

>>> symbols2digits("Where wolf's ears are, wolf's teeth are near.", key)
'263863356368227752646124686325352468253563876822775264612468326363323868253563689463253527'
>>> symbols2digits("Where wolf's ears are, wolf's teeth are near.", key, swap=True)
'628336533686227725461642863652534286525336788622772546164286233636238386525336864936525372'

>>> grid = make_grid(key)
>>> grid
{1: 'mZkqUpMKE', 2: 'BwRsaW.DQ', 3: '|tVCr7Th"', 4: 'yG%_u#L(&', 5: '3lXHIcOPi', 6: "'-efY9$ 2", 7: 'jS80@zo:b', 8: ')g;N54,xd', 9: 'J1Fn?Av6!'}

>>> digits2symbols('263863356368227752646124686325352468253563876822775264612468326363323868253563689463253527', grid)
"Where wolf's ears are, wolf's teeth are near."
>>> digits2symbols('628336533686227725461642863652534286525336788622772546164286233636238386525336864936525372', grid, swap=True)
"Where wolf's ears are, wolf's teeth are near."

>>> encode("Where wolf's ears are, wolf's teeth are near.", key)
'-;7X74woa#pG47lXG4lX7:4woa#pG4R77R;4lX74&7lXS'

>>> decode('-;7X74woa#pG47lXG4lX7:4woa#pG4R77R;4lX74&7lXS', key)
"Where wolf's ears are, wolf's teeth are near."

Epilogue

The valknut-cipher owes its name to the form in which the key of the cipher is normally displayed. The valknut (Old Norse; valr: fallen warriors + knut: knot) is a symbol consisting of three interlocked triangles. It appears on a wide variety of objects found in areas inhabited by the Germanic peoples, usually along with references to the god Odin⁵. That is why it is also called the Odin's or Wodans' knot. The valknut appears prominently on two 8th century picture stones⁶ from Gotland⁷, Sweden: the Tängelgarda stone⁸ and the Stora Hammar stone⁹. But it is also found on a ring that was found in the English river Nene¹⁰ and on the Oseberg ship¹¹ that is on display in the Norwegian Vikingskipshuset museum¹².

The valknut representation of a key has a triangle in the center containing the nine digits 1–9, surrounded by three trapezoids containing the 81 symbols. Each trapezoid itself consists of three triangles containing nine symbols each, accounting for 27 symbols per trapezoid.

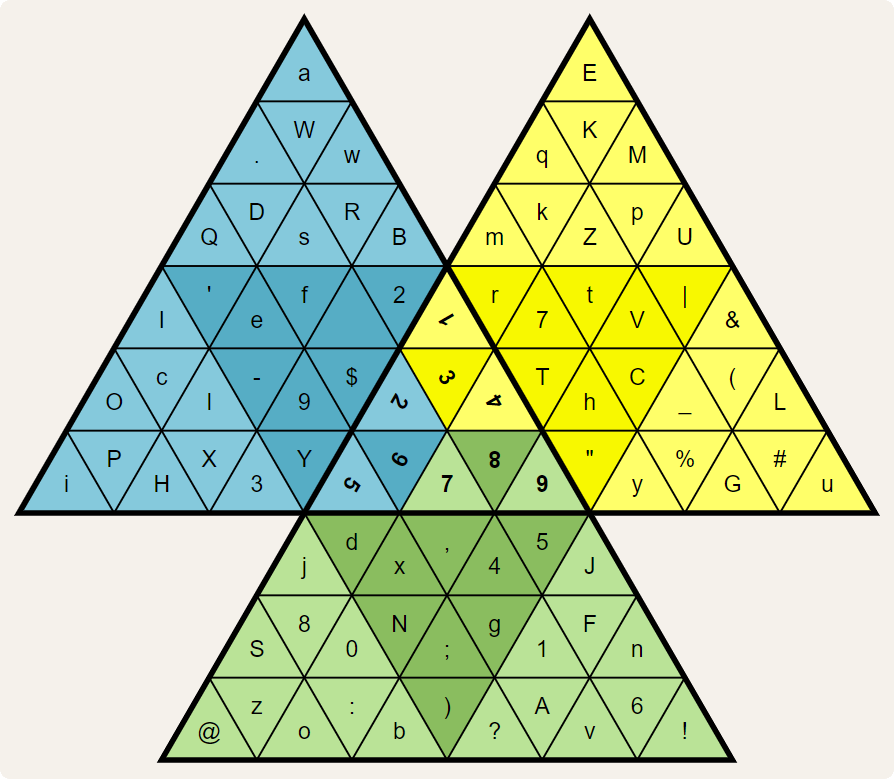
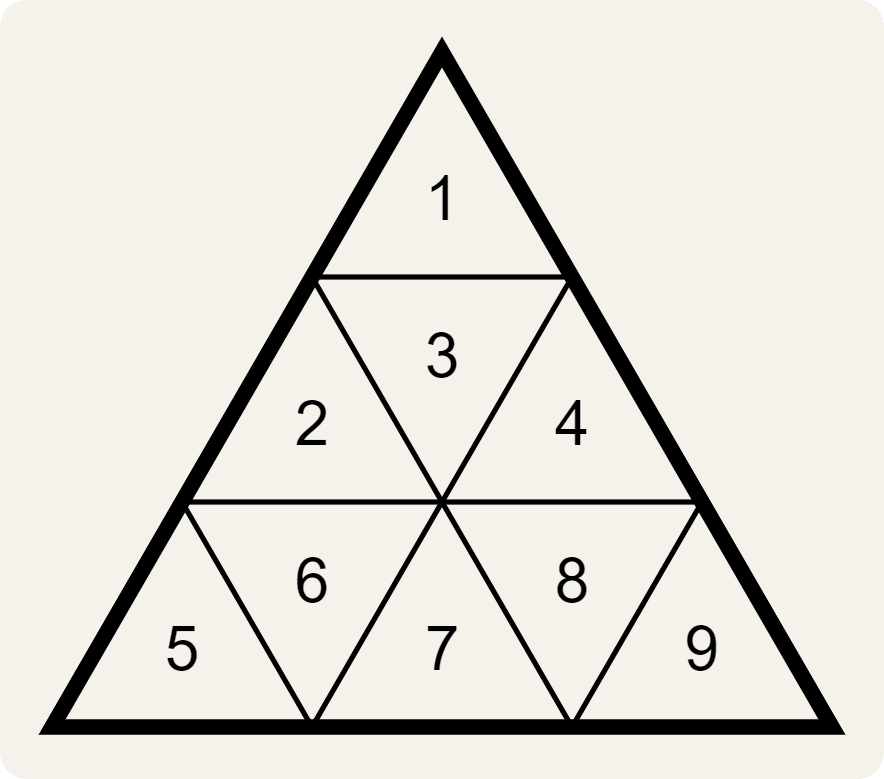
The valknut representation of a key thus consists of 10 triangles: 1 triangle filled with digits in the center and 9 triangles filled with symbols that in triplets form one trapezoid. Each of these triangles contains nine digits/symbols. The nine digits/symbols in a triangle are numbered in reading order (left to right, and top to bottom) with the nine digits 1–9.

Each digit pair $$ij$$ ($$1 \leq i, j \leq 9$$) then corresponds to one symbol $$\alpha$$ that appears in one of the trapezoids of the key. To find that corresponding symbol, look for the digit $$i$$ in the center triangle of the key. Those digits indicate which triangle in the trapezoids the digit $$i$$ corresponds to. The blue trapezoid containing the digits 265 inside the center triangle is congruent with the blue trapezoid at the top left. The rotation of digits 2, 6 and 5 indicates the direction in which the triangles inside the blue trapezoid should be read. Similarly, digits 7, 8 and 9 correspond to the triangles in the green trapezoid at the bottom, and digits 1, 3 and 4 to the triangles in the yellow trapezoid at the top left.

Once we have found which triangle in the trapezoids digit $$i$$ corresponds to — and in which direction we should read that triangle — then digit $$j$$ indicates the number of symbol $$\alpha$$ in that triangle. As such, the two digits 26 correspond to symbol W. The first digit $$i=2$$ leads us to the upper light blue triangle in the blue trapezoid. If we read out that triangle in the same direction in which the digit 2 is rotated in the center triangle of the key, we get the sequence of symbols BwRsaW.DQ. At position $$j=6$$ of that sequence is the symbol W we were looking for.

The valknut representation therefore corresponds to the grid representation of a valknut-key, but requires a bit more effort to retrieve the corresponding symbol for a digit pair.