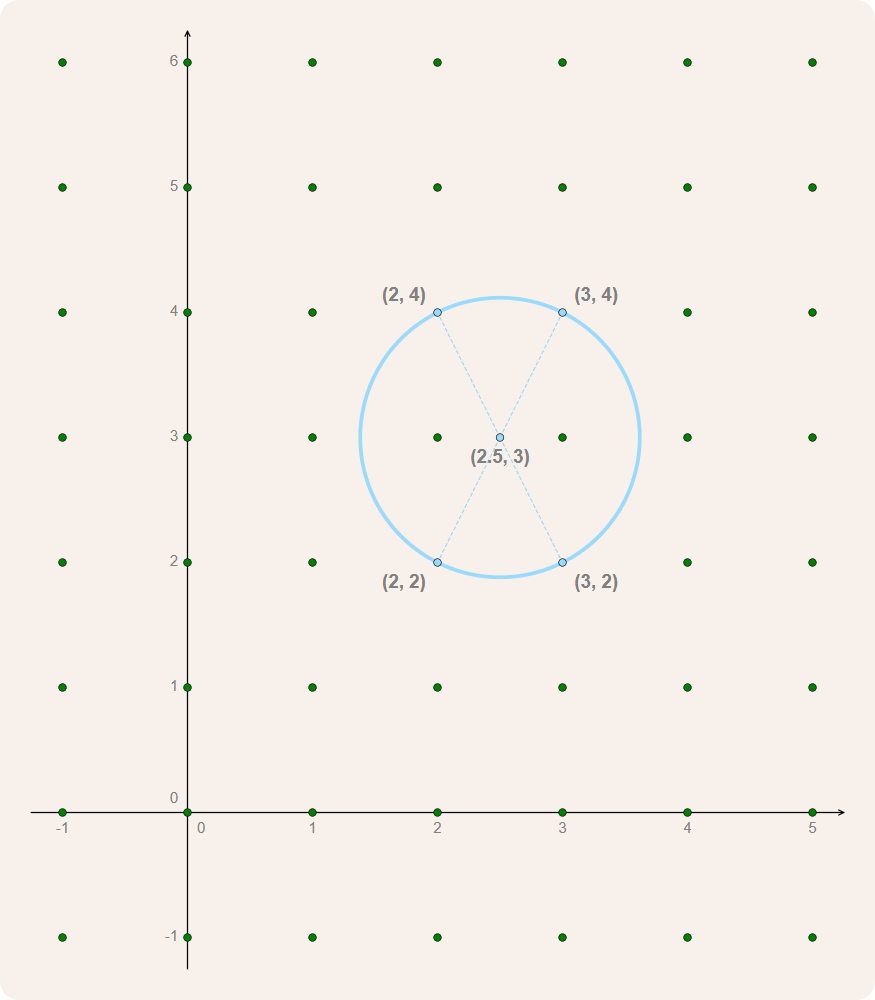
For any positive integer $$n \in \mathbb{N}$$, there exists a circle that passes through exactly $$n$$ lattice points in the Euclidean plane. This was first proven by Polish mathematician Andrzej Schinzel1 in 1958. For example, the circle with center $$(2.5, 3)$$ and radius $$\frac{\sqrt{5}}{2}$$ passes through the four lattice points $$(2, 4)$$, $$(3, 4)$$, $$(3, 2)$$ and $$(2, 2)$$.
Assignment
We represent a point in the Euclidean plane as a tuple $$(x, y)$$ with $$x, y \in \mathbb{R}$$ (float).
A latice point is a point with integer coordinates. We represent a lattice point as a tuple $$(x, y)$$ with $$x, y \in \mathbb{Z}$$ (int).
A point $$(x, y)$$ is on a circle with center $$(m_x, m_y)$$ and radius $$r$$ if and only if \[ (x - m_x)^2 + (y - m_y)^2 = r^2 \]
Comparing real numbers
When working with floating point numbers, it is unsafe to directly compare two numbers $$a \in \mathbb{R}$$ (float) and $$b \in \mathbb{R}$$ (float). Instead, we say that $$a$$ and $$b$$ are equal if $$|a - b| < \epsilon$$. Here, $$|x|$$ represents the absolute value of $$x \in \mathbb{R}$$ and $$\epsilon \in \mathbb{R}$$ is a very small value called the tolerance. In this assignment, we use $$\epsilon = 10^{-6}$$ as the tolerance.
The bounding box of a circle is the rectangle with lower-left corner point $$(\left \lfloor{m_x - r}\right \rfloor, \left \lfloor{m_y - r}\right \rfloor)$$ and upper-right corner point $$(\left \lceil{m_x + r}\right \rceil, \left \lceil{m_y + r}\right \rceil)$$. Here, $$\left \lfloor{x}\right \rfloor$$ represents the greatest integer less than or equal to $$x \in \mathbb{R}$$ and $$\left \lceil{x}\right \rceil$$ represents the least integer greater than or equal to $$x \in \mathbb{R}$$. For example, the circle with center $$(2.5, 3)$$ and radius $$\frac{\sqrt{5}}{2}$$ has a bounding box with lower-left corner point $$(1, 1)$$ and upper-right corner point $$(4, 5)$$.
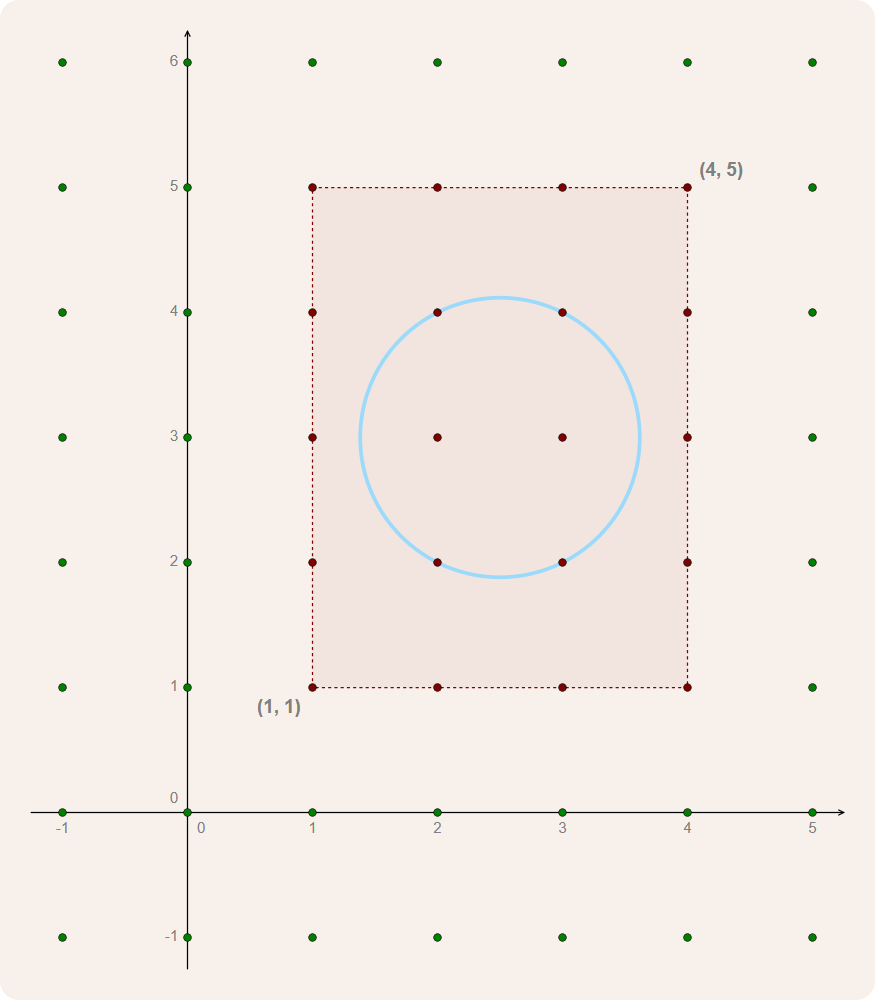
To determine which lattice points are on a circle with center $$(m_x, m_y)$$ and radius $$r$$, we can check all lattice points inside its bounding box to see if they are on the circle.
Your task:
-
Write a function point_on_circle that takes three arguments: i) a point $$p$$ (tuple), ii) the center $$c$$ (tuple) of a circle and iii) the radius $$r$$ (float) of the circle. The function must return a Boolean value (bool) that indicates whether point $$p$$ is on the circle with center $$c$$ and radius $$r$$.
-
Write a function bounding_box that takes the center $$c$$ (tuple) and the radius $$r$$ (float) of a circle. The function must return a tuple with the lower-left corner point (tuple) and the upper-right corner point (tuple) of the bounding box of the circle with center $$c$$ and radius $$r$$.
-
Write a function lattice_points that takes the center $$c$$ (tuple) and the radius $$r$$ (float) of a circle. The function must return a set containing all lattice points (tuple) that are on the circle with center $$c$$ and radius $$r$$.
Example
>>> point_on_circle((2.0, 4.0), (2.5, 3.0), 5 ** 0.5 / 2)
True
>>> point_on_circle((1.0, 3.0), (2.5, 3.0), 5 ** 0.5 / 2)
False
>>> bounding_box((2.5, 3.0), 5 ** 0.5 / 2)
((1, 1), (4, 5))
>>> bounding_box((4 / 3, 2.0), 5 ** 2 / 3)
((-8, -7), (10, 11))
>>> lattice_points((2.5, 3.0), 5 ** 0.5 / 2)
{(2, 4), (3, 2), (3, 4), (2, 2)}
>>> lattice_points((4 / 3, 2.0), 5 ** 2 / 3)
{(8, 7), (8, -3), (-1, 10), (-1, -6), (-7, 2)}
Resources
-
Schinzel A (1958). Sur l'existence d'un cercle passant par un nombre donné de points aux coordonnées entieres. Heritage of European Mathematics 4(1), 17. 2
-
Honsberger R (1973). Schinzel's theorem. Mathematical Gems I, Dolciani Mathematical Expositions, vol. 1, Mathematical Association of America 3