The method to determine the zeroes of a quadratic function ($$ax^2 + bx + c = 0$$) is exact and well-known ($$\Delta = b^2 - 4ac, \ldots$$). The calculations become more complex when determining the zeroes of a cubic or quartic function. For quintic and higher degree functions, no formula exists to calculate their zeroes. In these cases, it has even been proven¹ that a general formula will never be found.

Let this not discourage you. Although the positions of the zeroes cannot exactly be determined, we're still able to approximate them. Further, as the accuracy of floating point number representations within computers is limited, we can iteratively calculate the zeroes until the difference between the real zeroes and the estimated zeroes becomes smaller than the accuracy of the computer. 

The best known method to approximate the zeroes of a function is Newton's method². This method starts with an initial approximation $$x_1$$ of a zero. Once an estimation $$x_n$$ ($$n = 1, 2, \ldots$$) is obtained, a new one $$x_{n+1}$$ that is more accurate than the previous one is calculated by determining the intersection of the tangent to the function at the point $$x_n$$ with the $$X$$ axis. This procedure is repeated, until a sufficiently accurate approximation is obtained.

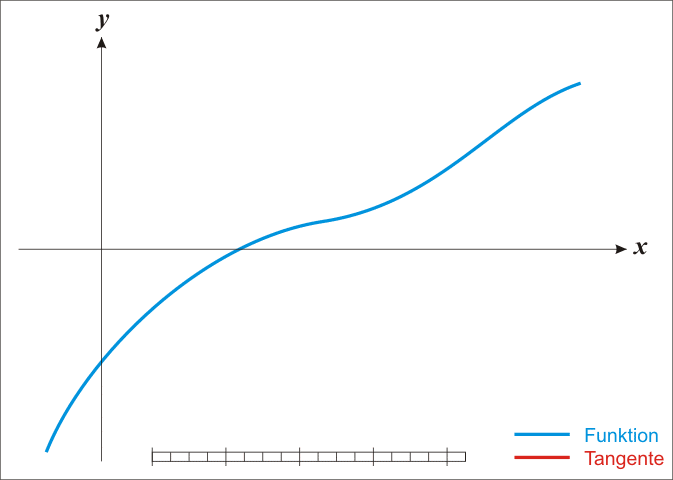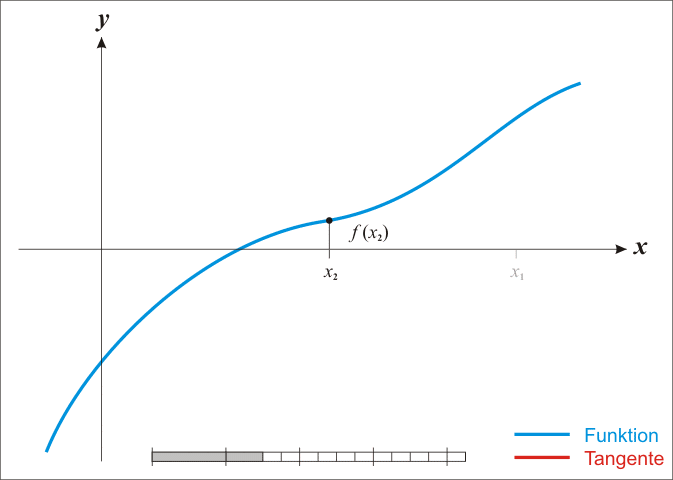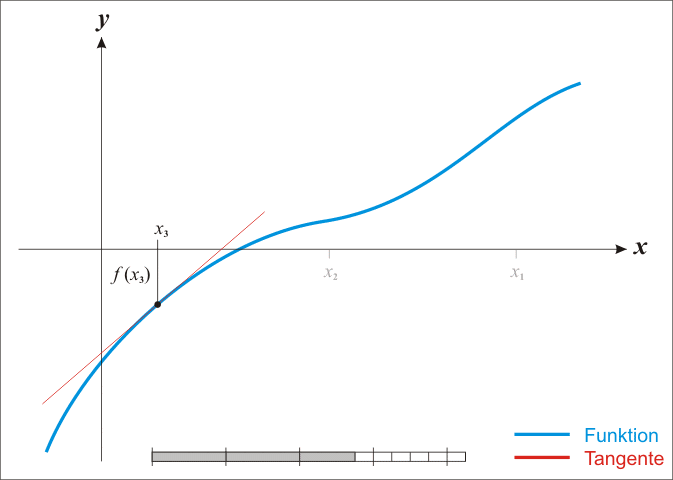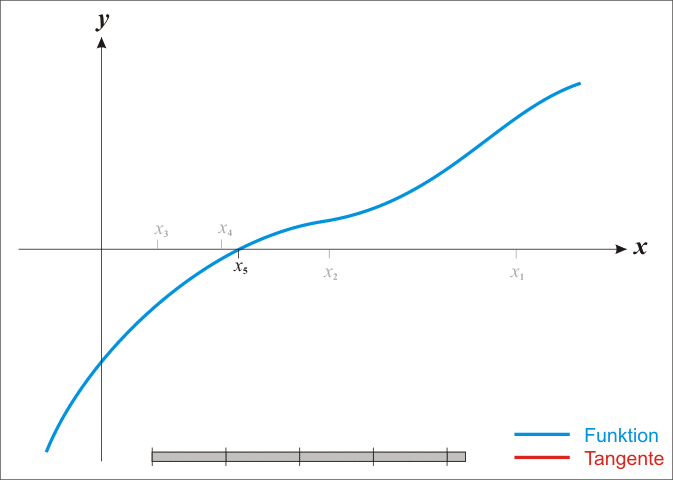
In case an estimation $$x_n$$ of a zero is known, the next estimation may be determined as $$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$. Here, $$f'$$ is the derivative of the function $$f$$, so that $$f'(x)$$ denotes the slope of the tangent to the function $$f$$ in the point $$x$$. To find a good approximation of a zero using Newton's method, it is important to have an initial estimate $$x_1$$ that is positioned close enough to the zero (how close depends on the function itself). The series of estimates should continue until $$f(x_m)$$ is close enough to zero.

Exercise

The Van der Waals force³ $$E$$ between two atoms in an inert gas can be written in function of the distance $$r$$ between the atoms \[E(r) = \frac{A}{r^{12}} - \frac{B}{r^6}\] in which $$A$$ and $$B$$ represent two gas constants that need to be determined experimentally. For this exercise, apply Newton's method to find the distance between two atoms where $$E = 100$$. In other words, search the zero of the function $$f(r) = E(r) - 100$$. The derivative of this function is: \[f'(r) = -\frac{12 A}{r^{13}} + \frac{6 B}{r^7}\]

Input

The input consists of three real numbers, each on a separate line. The first two lines represent the experimentally determined gas constants $$A$$ and $$B$$. De third line contains an initial estimation $$r_1$$ of the distance with $$E(r_1) \approx 100$$.

Output

The first estimation $$r_m$$ resulting from the application of Newton's method that meets $$|E(r_m) - 100| \le \epsilon$$, with $$\epsilon = 10^{-8}$$. This estimation is accurate up to 8 digits behind the decimal sign.

Example

Input:

1.5
7.12
0.5

Output:

0.6718209666720478