We have thus far worked with theoretical spectra of cyclic peptides1, in which the mass of every subpeptide is given. This inflexibility presents a practical barrier, since mass spectrometers2 generate spectra that are far from ideal — they are characterized by having both false masses and missing masses. A false mass is present in the experimental spectrum but absent from the theoretical spectrum. A missing mass is present in the theoretical spectrum but absent from the experimental spectrum (see figure below).

false and missing masses
Theoretical and simulated experimental spectra for NQEL. False masses are shown in green, and masses missing from the experimental spectrum are shown in blue.

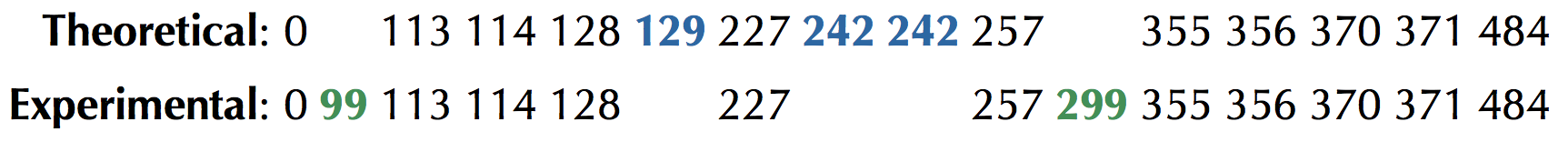
To generalize "Find a cyclic peptide with a given ideal spectrum3" to handle "noisy" spectra having false and missing masses, we need to relax the requirement that a candidate peptide's theoretical spectrum must match the experimental spectrum exactly, and instead incorporate a scoring function that will select the peptide whose theoretical spectrum matches the given experimental spectrum the most closely. Given a cyclic peptide $$p$$ and a spectrum $$s$$, we define ScoreC($$p$$, $$s$$) as the number of masses shared between Cyclospectrum($$p$$) and $$s$$. Recalling the figure above, if

$$s$$ = {0, 99, 113, 114, 128, 227, 257, 299, 355, 356, 370, 371, 484}

then

ScoreC(NQEL, $$s$$) = 11

To limit the number of candidate peptides under consideration, we will use a Leaderboard, which holds the $$N$$ highest scoring candidate peptides for further extension. At each step, we will expand all candidate peptides found in Leaderboard by adding every possible amino acid to the end. Then, we will eliminate those peptides whose newly calculated scores are not high enough to keep them on the Leaderboard. This idea is similar to the notion of a cut in a golf tournament. After the cut, only the top $$N$$ golfers are allowed to play in the next round, since they are the only players who have a reasonable chance of winning.

To be fair, a cut should include anyone who is tied with the $$N$$-th place competitor. Thus, Leaderboard should be trimmed down to the "$$N$$ highest-scoring peptides including ties", which may include more than $$N$$ peptides. Given a list of peptides Leaderboard, an integer N and spectrum $$s$$, Cut(Leaderboard, $$N$$, $$s$$) returns the top $$N$$ highest-scoring peptides in Leaderboard (including ties) with respect to spectrum $$s$$. We now introduce LeaderboardCyclopeptideSequencing. In what follows, the 0-peptide is the peptide containing no amino acids.

LeaderboardCyclopeptideSequencing(N, Spectrum)
    Leaderboard ← {0-peptide}
    LeaderPeptide ← 0-peptide
    while Leaderboard is non-empty
        Leaderboard ← Expand(Leaderboard)
        for each Peptide in Leaderboard
            if Mass(Peptide) = ParentMass(Spectrum)
                if ScoreC(Peptide, Spectrum) > ScoreC(LeaderPeptide, Spectrum)
                    LeaderPeptide ← Peptide
            else if Mass(Peptide) > ParentMass(Spectrum)
                remove Peptide from Leaderboard
        Leaderboard ← Cut(Leaderboard, N, Spectrum)
    output LeaderPeptide

Assignment

Write a function leaderboard_cyclopeptide_sequencing that takes an integer $$N$$ and a spectrum $$s$$. The function must return LeaderPeptide after running  LeaderboardCyclopeptideSequencing($$N$$, $$s$$).

Example

>>> leaderboard_cyclopeptide_sequencing(10, (0, 71, 113, 129, 147, 200, 218, 260, 313, 331, 347, 389, 460))
(71, 147, 113, 129)

Note

The peptide scoring function in LeaderboardCyclopeptideSequencing currently assumes that peptides are circular, but peptides on the leaderboard should technically be scored as linear peptides until the final step. How would you score a linear peptide against a spectrum?

Resources