A curiosity attributed to Professor E. Ducci in the 1930s.
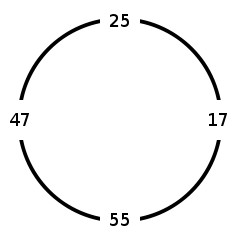
Arrange four non-negative integers in a circle, as above. Now construct another cyclic quadruple of integers by subtracting consecutive pairs, always subtracting the smaller number from the larger number. So the quadruple above would produce a new quadruple 22–8–38–8. If we apply the procedure to this new quadruple, we obtain another quadruple 14–30–30–14, and so on. Ducci found that eventually four equal numbers will occur. A proof appears in Ross Honsberger's Ingenuity in Mathematics (1970).
Input
Four integers, each on a separate line.
Output
The given quadruple of integers is arranged in a circle, with the first integer at the leftmost position and the following integers clockwise around the circle. Then we apply the procedure of Ducci and again arrange the newly obtained quadruple around a circle. The leftmost integer in the new circle indicates the difference between the leftmost and topmost integers in the original circle, the topmost integer in the new circle indicates the difference between the topmost and rightmost integers in the original circle, and so on clockwise around the circle.
The output should contain the sequence of cyclic quadruples obtained when applying the procedure of Ducci to the four given integers. The first circle should represent the cyclic quadruple containing the four given integers, and the last circle should represent the first cyclic quadruple that has four equal integers. For each circle in the sequence, a single line of output must be generated that contains the four integers in the order left-top-right-bottom, separated from each other by dashes (-).
Example
Input:
47
25
17
55Output:
47-25-17-55
22-8-38-8
14-30-30-14
16-0-16-0
16-16-16-16