The diffy game is great for practicing subtraction, but it also requires students to think logically and identify patterns. It can be played with integers, fractions, decimals and money, but most often it is played with natural numbers.

Game board of the diffy game.

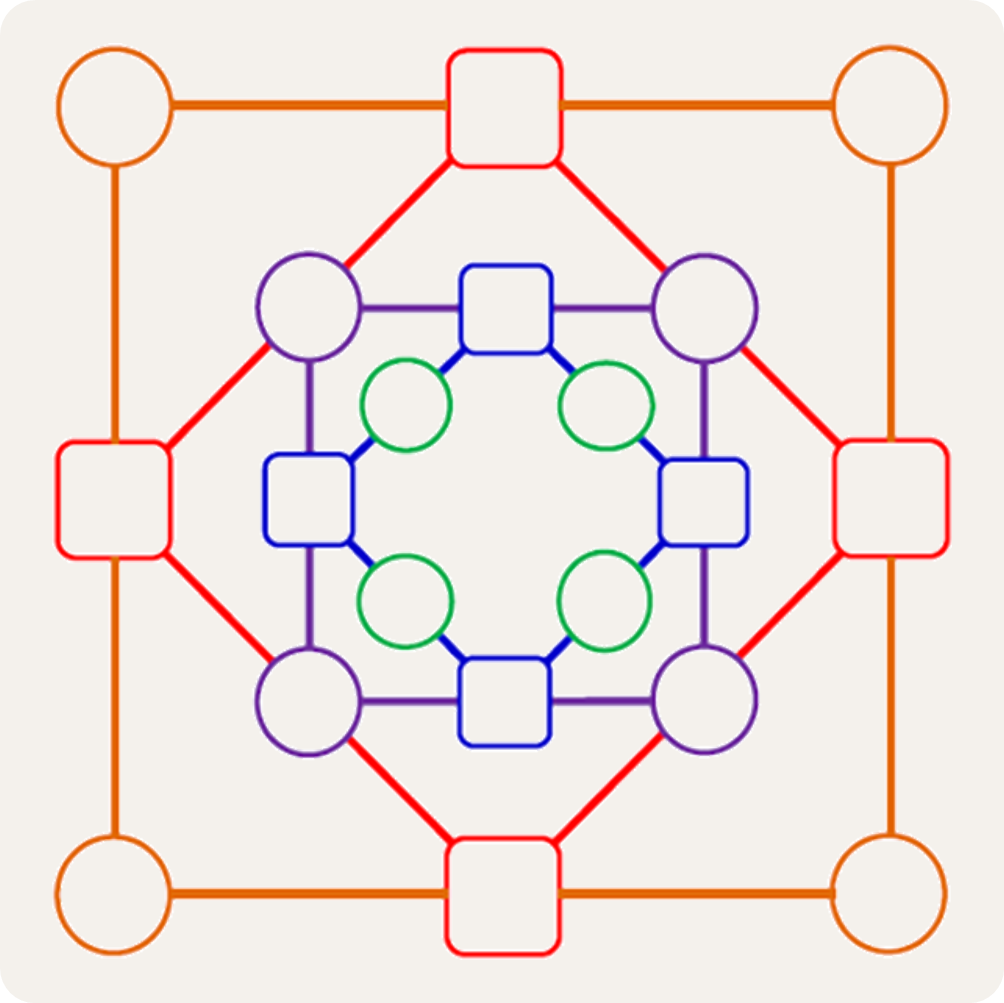
The game begins by writing four random numbers into the four circles on each of the outer corners. Then, the outer squares are filled in by subtracting the smaller number from the larger number on each neighbouring corner. This procedure in which neighbouring corners are subtracted is repeated towards the center. What patterns do you observe? Can you get to the center without any zero differences?

Completed example of a diffy game.

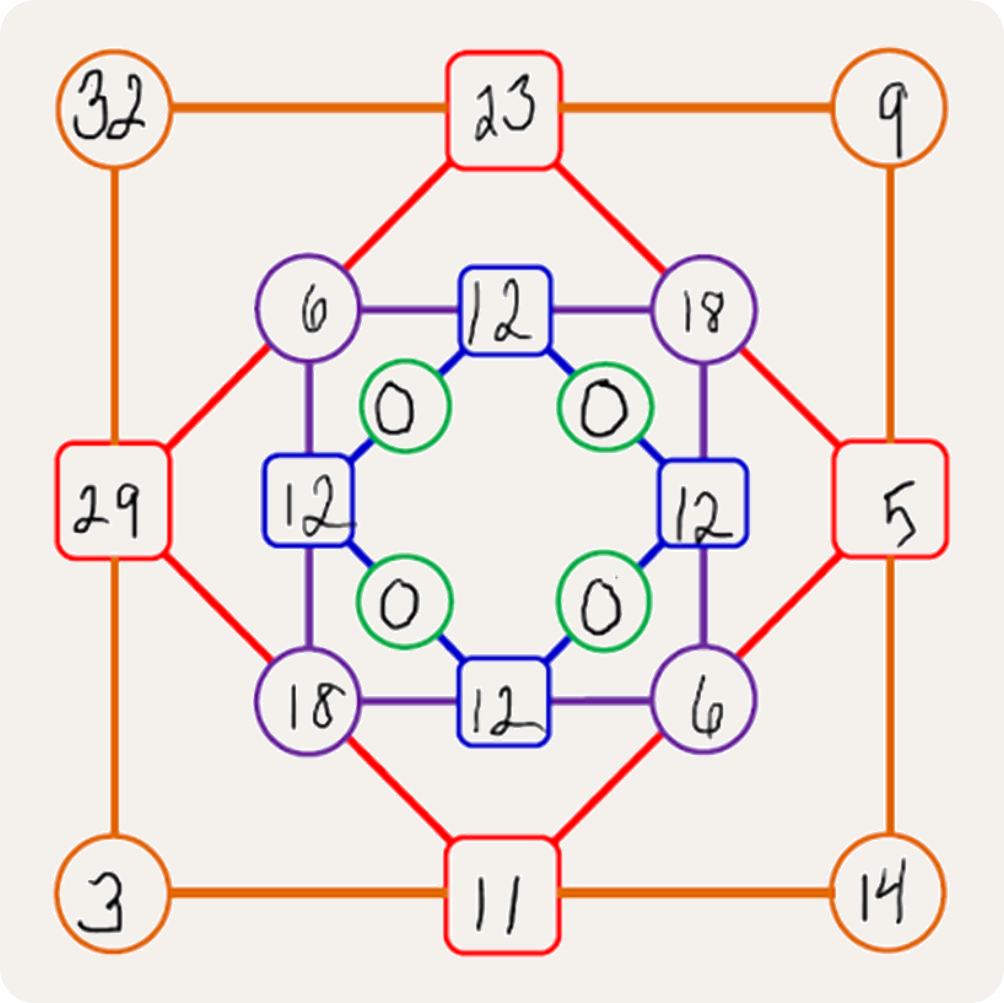
The above figure shows a completed example of a diffy game. As you can see, the player did not win because the circles closest to the center all came up zero. Is it possible to win this game?

Assignment

The diffy game is a special case of a Ducci sequence, named after the Italian mathematician Enrico Ducci who is credited with the discovery of this sequence of $$n$$-tuples of integers. Given an $$n$$-tuple of integers $$(a_1, a_2, \ldots, a_n)$$, the next $$n$$-tuple in the sequence is formed by taking the absolute differences of neighbouring integers: \[(a_1, a_2, \ldots, a_n) \rightarrow (|a_1 - a_2|, |a_2 - a_3|, \ldots, |a_{n - 1} - a_n|, |a_n - a_1|)\] This procedure assumes that the last integer in the $$n$$-tuple is followed by the first integer. Another way of describing the progression of the sequence is as follows. Arrange $$n$$ integers in a circle and make a new circle by taking the difference between neighbours, ignoring minus signs. Then repeat the operation.

Because every Ducci sequence of integers eventually will repeat itself (a property that is easily proven), Ducci sequences are periodic. Each Ducci sequence will eventually reach an $$n$$-tuple of zeros (in this case the period is equal to zero), or an $$n$$-tuple that previously occurred in the Ducci sequence (in this case the period equals the number of $$n$$-tuples before repetition occurs). For example, consider the following Ducci sequence: \[\begin{matrix} (1, 2, 1, 2, 1, 1) & \rightarrow & \mathbf{(1, 1, 1, 1, 0, 0)} & \rightarrow & \mathbf{(0, 0, 0, 1, 0, 1)} & \rightarrow \\ \mathbf{(0, 0, 1, 1, 1, 1)} & \rightarrow & \mathbf{(0, 1, 0, 0, 0, 1)} & \rightarrow & \mathbf{(1, 1, 0, 0, 1, 1)} & \rightarrow \\ \mathbf{(0, 1, 0, 1, 0, 0)} & \rightarrow & (1, 1, 1, 1, 0, 0) & \rightarrow & \cdots & \\ \end{matrix}\] The first repetition occurs when the tuple $$(1, 1, 1, 1, 0, 0)$$ pops up in the sequence a second time. To make this clear, we have highlighted all tuples that are part of the first period using bold face text. The period of this Ducci sequence may thus be determined by counting the number of steps needed to progress from the first occurrence of the tuple $$(1, 1, 1, 1, 0, 0)$$ to the second occurrence of this tuple. In this case, the period is equal to six.

Your task:

Write a function next that takes a sequence (list or tuple) of $$n \in \mathbb{N}_0$$ integers (int). The function must return the $$n$$-tuple (tuple) of integers (int) that follows the given sequence in a Ducci sequence.
Write a function ducci that takes a sequence (list or tuple) of $$n \in \mathbb{N}_0$$ integers (int). The function must return the Ducci sequence (tuple) that starts with the given $$n$$-tuple (tuple) and continues repeatedly with the next $$n$$-tuple (tuple) in the Ducci sequence. The sequence either ends in the first $$n$$-tuple of zeros or the first $$n$$-tuple that occurs twice in the Ducci sequence.
Write a function period that takes a sequence (list or tuple) of $$n \in \mathbb{N}_0$$ integers (int). The function must return the period (int) of the Ducci sequence that starts with the given $$n$$-tuple.

Example

>>> next([32, 9, 14, 3])
(23, 5, 11, 29)
>>> next((1, 2, 1, 2, 1, 0))
(1, 1, 1, 1, 1, 1)
>>> next((1, 2, 1, 2, 1, 1))
(1, 1, 1, 1, 0, 0)

>>> ducci([32, 9, 14, 3])
((32, 9, 14, 3), (23, 5, 11, 29), (18, 6, 18, 6), (12, 12, 12, 12), (0, 0, 0, 0))
>>> ducci((1, 2, 1, 2, 1, 0))
((1, 2, 1, 2, 1, 0), (1, 1, 1, 1, 1, 1), (0, 0, 0, 0, 0, 0))
>>> ducci((1, 2, 1, 2, 1, 1))
((1, 2, 1, 2, 1, 1), (1, 1, 1, 1, 0, 0), (0, 0, 0, 1, 0, 1), (0, 0, 1, 1, 1, 1), (0, 1, 0, 0, 0, 1), (1, 1, 0, 0, 1, 1), (0, 1, 0, 1, 0, 0), (1, 1, 1, 1, 0, 0))

>>> period([32, 9, 14, 3])
0
>>> period((1, 2, 1, 2, 1, 0))
0
>>> period((1, 2, 1, 2, 1, 1))
6