Plaintext and ciphertext are two concepts from cryptography — from Ancient Greek: κρυπτός (kryptós, "hidden, secret") and γράφειν (gráphein, "to write") —the practice and study of techniques for secure communication in the presence of adversarial behavior. Prior to the modern age, cryptography was effectively synonymous with encryption, the process of converting human readable information (plaintext) to unintelligible nonsense text (ciphertext), which can only be read by reversing the process (decryption). The terms encryption (converting plaintext to ciphertext) and decryption (converting ciphertext to plaintext) have distinct meanings within cryptography.
The terms ciphertext, encipher and decipher are somewhat confusing as a ciphertext may indeed consist of digits (ciphers), but that is not always the case. They are derived from the term "cipher" — a pair of algorithms to carry out encryption and the reversing decryption. The detailed operation of a cipher is controlled both by the algorithm and a "key": a secret string of characters (ideally short so it can be remembered easily) that is needed to decrypt the ciphertext.
Other terms are encoding and decoding, but these are equally confusing because there are many codes that are not secret at all, such as Morse code1.
Assignment
The Bernina cipher is a cryptographic technique in which the key and ciphertext have the same length (the same number of characters). Decryption is done by putting the key on top of the ciphertext. We'll use this key and ciphertext as an example:
key: π = 3.14159265358979323846264338327950288419716939 ciphertext: BR7Ih4h a aideipoor rfi1tes0ir s fdgWtin0te rt?
First, we scan the ciphertext from left to right to find all characters that are below a digit 0 in the key. In our example, this is just the capital W. Next, we scan the ciphertext from left to right to find all characters that are below a digit 1 in the key. In our example, this is the case for the letters h, a, t and a space. We repeat this procedure for digits 2–9:
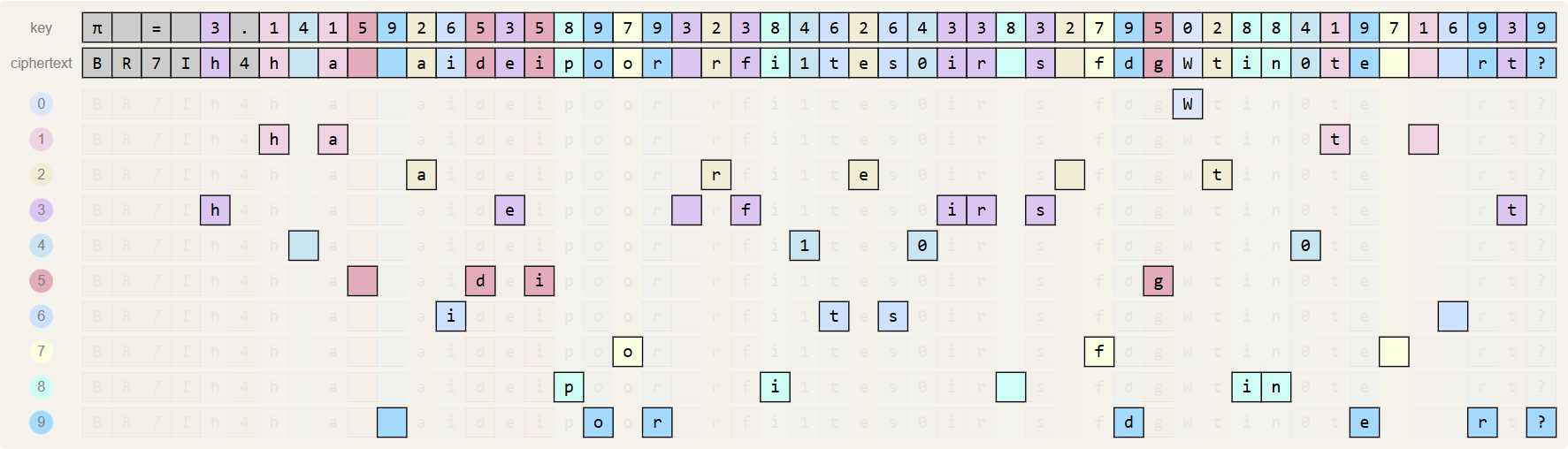
The plaintext is obtained by stringing all these characters together. For our the example we get:
011112222233333333444455556666777888889999999 plaintext: What are the first 100 digits of pi in order?
On top of each character in the plaintext we have put its corresponding digit in the key. Note that the Bernina cipher does not add characters from the ciphertext to the plaintext if they don't correspond with a digit in the key. As a result, the plaintext may be shorter than the ciphertext and the key. We have marked these characters with gray background color in the figure above.
Input
The first line contains a key. The second line contains a ciphertext that was encrypted with the Bernina cipher and the key from the first line. Both lines contain the same number of characters.
Output
The plaintext obtained by decrypting the ciphertext with the Bernina cipher and the given key.
Example
Input:
π = 3.14159265358979323846264338327950288419716939
BR7Ih4h a aideipoor rfi1tes0ir s fdgWtin0te rt?Output:
What are the first 100 digits of pi in order?Epilogue
South of Brusio2 — in the Swiss Canton of Graubünden3 — the Bernina railway4 must change elevation without exceeding its specified maximum gradient of 7 percent. So engineers adopted the appealing expedient of a spiral viaduct, an arch bridge of nine spans that carries a train through 360 degrees with a grade gentle enough to ensure safety. Opened in 1908, it was recognized as a UNESCO World Heritage Site5 in 2008.

The name of the Bernina cipher refers to this ingenious solution, as decryption requires spiraling through the ciphertext over and over again to select characters corresponding to the next digit in the key.