We have already applied linear interpolation in a previous assignment¹ to estimate the missing measurements of a function $$y = f(x)$$ on the basis of known measurements. We assumed that the function was measured for the $$x$$-values 1, 2, …, 100.

In this assignment we will extend this technique for a variable number of measurement points $$x_i$$ ($$1 \leq i \leq n$$) which do not necessarily coincide with the integers, and which may even have different distances between them. The only thing we assume is that $$x_i < x_j$$ is always valid if $$i < j$$, in other words, that increasing $$x$$-values were applied when measuring (or that the measurements were sorted in that order).

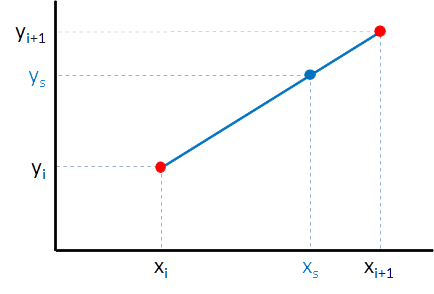
To estimate the value $$y_s = f(x_s)$$ which matches the $$x$$-value $$x_s$$ — which lies between the successive $$x$$-values $$x_i$$ and $$x_{i+1}$$ — we still use the formula for linear interpolation: \[ y_s = y_i + (x_s-x_i)\frac{(y_{i+1}-y_i)}{(x_{i+1}-x_i)} \]

Assignment

Write a function interpolation to which two arguments must be passed. The first argument is a list of measurement points, where each measurement point is represented as a tuple $$(x, y)$$ where $$x, y \in \mathbb{R}$$. The second argument is a number l $$x_s \in \mathbb{R}$$. If the $$x$$-values of the given measurement points are not give in ascending order, then the function should return the string 'invalid input'. If the given $$x$$-value $$x_s$$ is not within the range of the measurement points ($$x_s < x_1$$ of $$x_s > x_n$$), then the function should return the string 'out of range'. Otherwise the function should return the $$y$$-value $$y_s \in \mathbb{R}$$ that, according to the principle of linear interpolation, corresponds with the given $$x$$-value $$x_s$$. 

Example

>>> interpolation([(4.88, -2.15), (6.42, -0.45), (6.99, 3.93), (7.69, -3.64)], 5.45)
-1.5207792207792203
>>> interpolation([(3.3, 1.26), (4.25, -0.27), (6.17, 3.53), (8.16, 2.47)], 8.11)
2.496633165829146
>>> interpolation([(2.24, 1.66), (3.5, 0.43), (3.96, -0.57), (4.35, -0.25)], 5.56)
'out of range'
>>> interpolation([(2.61, -1.97), (1.66, -0.05), (3.33, -0.93), (5.18, -0.58)], 7.1)
'invalid input'