Genome assembly is the computational process in which the actual sequence of nucleotides making up an organism's genome is determined. Researchers are presently unable to read the nucleotides of an entire chromosome one at a time. Instead, they rely on high-technological chemical methods to determine the order of bases along short strands of DNA (usually less than 1000 bp). These short strands are called reads.
To sequence a genome, researchers chemically "blow up" multiple copies of a genome (typically taken from multiple cells of the same organism) into reads and then determine the nature of the reads. To reassemble the genome, they must use overlaps in reads to determine which read pairs are adjacent in the genome. For example, if the short reads GACCTACA and ACCTACAA are produced, then we might surmise from the fact that they overlap that they both belong to a substring GACCTACAA. An efficient algorithm for assembly that can handle all possible wrinkles and complications arising from practical concerns (such as errors in reads) still does not exist, so that research in genome assembly remains a highly competitive field.
Assignment
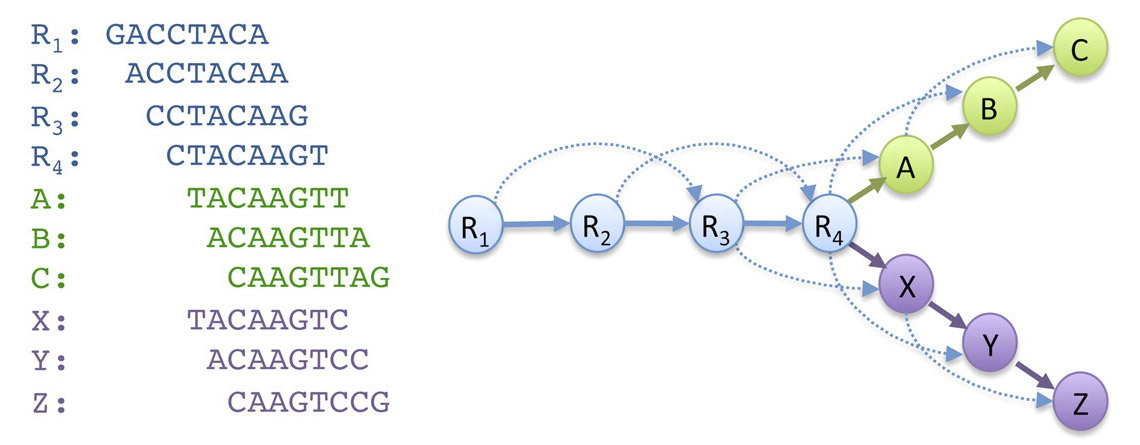
As a first step in genome assembly, most algorithms try to get insight in the overlap between reads by constructing an overlap graph. This is a data structure where overlapping reads (represented as labeled circles in the picture below) are connected using arrows. Note that it is possible that one read overlaps multiple other reads, usually due to repeats in the genome or sequencing errors. This causes so-called "forks" in the overlap graph.
The goal of this assignment is to construct the overlap graph for a given set of reads. In doing so, you proceed as follows:
Write a function overlap that takes three arguments. The first two arguments are reads, represented as strings that only contain the letters A, C, G and T (representing the four possible nucleotide bases). The third argument is an integer $$k \in \mathbb{N}_0$$. The function must return a Boolean value that indicates whether or not the first read has an overlap of length $$k$$ with the second read. This is the case if the first read ends in the same $$k$$ bases that are found at the start of the second read.
Use the function overlap to write a function maximalOverlap that takes two reads as its arguments. The function must return the length of the maximal overlap between the first and the second read. If the given reads don't overlap at all, the function must return the integer value zero.
Use the function maximalOverlap to write a function overlapGraph that takes two arguments: a collection (a list, tuple, set, …) of reads and an integer $$k \in \mathbb{N}_0$$. The function must return a dictionary that maps each read in the given collection onto the set of all other reads in the collection to which it overlaps with of a minimal length $$k$$ (in case this set isn't empty). One key-value pair of the dictionary thus represents the outgoing arrows of the overlap graph that start at a particular read (used as the key in the dictionary) and lead to all other reads that overlap with it. Note that by definition, an arrow never points from a read to the read itself, even though the read might overlap itself.
Example
>>> overlap('AAATTTT', 'TTTTCCC', 3)
True
>>> overlap('AAATTTT', 'TTTTCCC', 5)
False
>>> overlap('ATATATATAT', 'TATATATATA', 4)
False
>>> overlap('ATATATATAT', 'TATATATATA', 5)
True
>>> maximalOverlap('AAATTTT', 'TTTTCCC')
4
>>> maximalOverlap('ATATATATAT', 'TATATATATA')
9
>>> reads = ['AAATAAA', 'AAATTTT', 'TTTTCCC', 'AAATCCC', 'GGGTGGG']
>>> overlapGraph(reads, 3)
{'AAATTTT': {'TTTTCCC'}, 'AAATAAA': {'AAATTTT', 'AAATCCC'}}
>>> overlapGraph(reads, 4)
{'AAATTTT': {'TTTTCCC'}}
>>> reads = ['GACCTACA', 'ACCTACAA', 'CCTACAAG', 'CTACAAGT', 'TACAAGTT', 'ACAAGTTA', 'CAAGTTAG', 'TACAAGTC', 'ACAAGTCC', 'CAAGTCCG']
>>> overlapGraph(reads, 6)
{'CTACAAGT': {'ACAAGTCC', 'ACAAGTTA', 'TACAAGTC', 'TACAAGTT'}, 'TACAAGTT': {'CAAGTTAG', 'ACAAGTTA'}, 'ACCTACAA': {'CTACAAGT', 'CCTACAAG'}, 'ACAAGTCC': {'CAAGTCCG'}, 'ACAAGTTA': {'CAAGTTAG'}, 'GACCTACA': {'CCTACAAG', 'ACCTACAA'}, 'TACAAGTC': {'ACAAGTCC', 'CAAGTCCG'}, 'CCTACAAG': {'CTACAAGT', 'TACAAGTC', 'TACAAGTT'}}Note: the last example represents the overlap graph depicted in the introduction of this assignment.