On the 4th of July 1989, Soviet MiG-23 pilot Nikolai Skuridin was on a routine training flight near Kolobrzeg, Poland, when his afterburner failed. Skuridin ejected, thinking the engine was completely dead, but the plane recovered and proceeded on autopilot into the west.
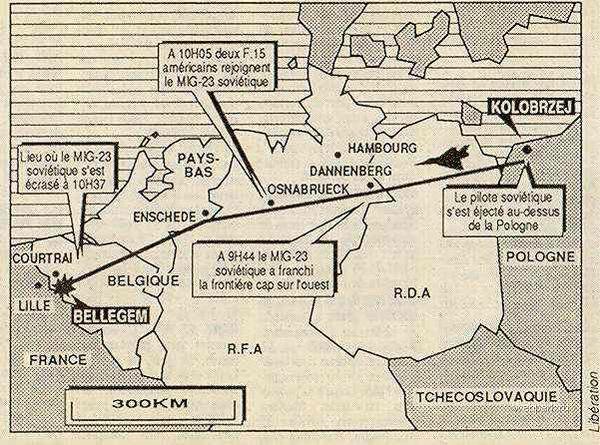
It must have had a lot of fuel, because it crossed out of Poland into East Germany, then into West Germany, then into the Netherlands, where a startled American air base sent up two F-15s to keep it company. As the MiG passed into Belgium the F-15s were told to shoot it down when it reached the North Sea, but it finally ran out of fuel near the French border, crashing into a house and killing a teenager.
The whole trip had covered 560 miles. Belgian Foreign Minister Mark Eyskens complained that the Soviets had issued no warning and no indication as to whether the pilotless plane was carrying dangerous weapons. It turned out that it was unarmed but carrying ammunition for a 23mm machine gun.
Assignment
Prior to departure, the pilot or flight dispatcher of an airplain must file a flight plan with the local aviation authority. This document generally includes basic information such as departure and arrival points, estimated time and route, alternate airports in case of bad weather, type of flight, number of people on board and information about the aircraft itself.
For this assignment, you are given a text file in CSV format (comma-separated values) containing information about a series of airports. The file contains twelve information fields for each airport. Of importance for this assignment is only the unique 3-letter code of the airport (first field), together with the latitude and longitude (fields 6 and 7 respectively) where the airport is located. Your task is to use the information in the text file to implement some simple route planning software that can determine the route for given airports of departure and arrival, and a given maximal range of the airplane.
Because it might well be that the distance between the airports of departure and arrival is larger than the range of the airplane, the route planning software might need to select some stopover airports where the airplane can refuel. The flight plan is determined by starting at the airport of departure, and then successively selecting the next unvisited airport within the range of the airplane that is closest to the destination (the airport of arrival). This procedure is repeated until the airport of arrival has been reached, or until no more airport can be reached that meets the required conditions.
In this assignment, locations on Earth are represented as tuples containing two floating point numbers, respectively representing the latitude and longitude of the location (expressed in degrees). These are called the coordinates of the location. To determine the distance between two airports having coordinates $$(b_1, l_1)$$ en $$(b_2, l_2)$$, we will make use of the Haversine distance $$d$$ between two points on a sphere that can be calculated by means of the following formula \[\begin{aligned}[c] a & = \left(\sin\left(\frac{b_2-b_1}{2}\right)\right)^2 + \cos(b_1)\cos(b_2)\left(\sin\left(\frac{l_2-l_1}{2}\right)\right)^2 \\ c & = \arctan\left(\sqrt{\frac{a}{1-a}}\right) \\ d & = 2rc \end{aligned}\] with $$r$$ equal to the radius of the sphere. Your task is to:
Write a function coordinates that takes the location of a CSV file as an argument. This file must contain information about a number of airports, in the format as described in the introduction of this assignment. The function must return a dictionary that maps the unique 3-letter code of each airport in the file onto the coordinates of the airport.
Write a function haversine that takes the coordinates of two locations as its arguments. The function must return the Haversine distance between the two locations, under the assumption that Earth is a sphere with radius $$r = 6371\mbox{ km}$$. Note that the trigonometric functions (sin, cos, ...) in the math module expect that angles are expressed in radians, not in degrees. However, the math module also has two functions degrees and radians that can be used to convert angles from radians to degrees, and vice versa.
Use the function haversine to write a function flightplan that can be used to determine the route of an airplane. Three arguments must be passed to the function. The first two arguments represent the unique 3-letter code of the airports of departure and arrival. The third argument is a dictionary mapping the unique 3-letter codes of airports onto their coordinates. In addition, the function has an extra optional parameter range that can be used to pass the range of the airplane (expressed in kilometers; default value: $$1000\mbox{ km}$$). The function must return the list of 3-letter codes of all airports the airplane will visit on its route from the airport of arrival to the airport of destination, in case the route planning algorithm given above is used. This means that the first and last airports in the list respectively are the airports of departure and arrival. In case the flight planning algorithm ends up in a situation where no more airports can be reached that meet the required conditions, the function must raise an AssertionError with the message no possible route.
CSV format
CSV format (comma-separated values) is a specification for storing tabular data (numbers and text) in plain text files. Each line of the file is a data record. Each record consists of one or more fields, separated by commas. The use of the comma as a field separator is the source of the name for this file format. Consider the following tabel as an example
| year | make | model | description | price |
|---|---|---|---|---|
| 1997 | Ford | E350 | airco, abs, moon | 3000.00 |
| 1999 | Chevy | Venture "Extended Edition" | 4900.00 | |
| 1999 | Chevy | Venture "Extended Edition, Very Large" | 5000.00 | |
| 1996 | Jeep | Grand Cherokee | MUST SELL! air, moon roof, loaded |
4799.00 |
The above table of data may be represented in CSV format as follows
Year,Make,Model,Description,Price
1997,Ford,E350,"ac, abs, moon",3000.00
1999,Chevy,"Venture ""Extended Edition""","",4900.00
1999,Chevy,"Venture ""Extended Edition, Very Large""",,5000.00
1996,Jeep,Grand Cherokee,"MUST SELL!
air, moon roof, loaded",4799.00This illustrates some additional rules that must be followed by CSV files:
the first row might contain the column headers, but this is not mandatory
any field may be enclosed within double quotes (")
fields containing commas, double quotes or newlines, or fields starting or ending with spaces should be enclosed within double quotes
a (double) quotein a field must be represented by two (double) quotes
In order not to take into account all these extra rules when processing CSV files, it is always a good option to use the csv module in Python, which is part of the Python Standard Library.
Example
The following interactie sessions assumes the text file airports.csv1 is located in the current directory.
>>> coords = coordinates('airports.csv')
>>> len(coords)
9187
>>> type(coords)
<class 'dict'>
>>> coords['BRU']
(50.902222, 4.485833)
>>> coords['CDG']
(49.016667, 2.55)
>>> coords['DCA']
(38.851944, -77.037778)
>>> coords['LAX']
(33.9425, -118.407222)
>>> haversine((50.902222, 4.485833), (49.016667, 2.55)) # BRU <-> CDG
251.2480027355068
>>> haversine((38.851944, -77.037778), (33.9425, -118.407222)) # DCA <-> LAX
3710.8262543589817
>>> flightplan('DCA', 'LAX', coords)
['DCA', 'MTO', 'HLC', 'BFG', 'LAX']
>>> flightplan('DCA', 'LAX', coords, range=2000)
['DCA', 'DDC', 'LAX']
>>> flightplan('DCA', 'LAX', coords, range=4000)
['DCA', 'LAX']
>>> flightplan('BRU', 'CDG', coords)
['BRU', 'CDG']
>>> flightplan('BRU', 'CDG', coords, range=50)
Traceback (most recent call last):
AssertionError: no possible route