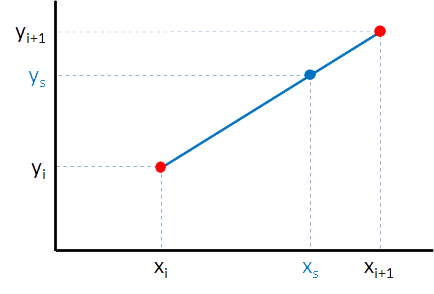
We have a table containing the $$y$$-values of a certain measurement, which match the $$x$$-values 1, 2, 3,…, 100. To estimate the $$y_s$$ result that matches the $$x$$-value $$x_s$$ — which lies between the successive whole $$x$$-values $$x_i$$ and $$x_{i+1}$$ — we use the formula for linear interpolation: \[ y_s = y_i + (x_s-x_i)\frac{(y_{i+1}-y_i)}{(x_{i+1}-x_i)} \]

example of linear interpolation

Assignment

Write a function linearInterpolation that takes two arguments. The first argument must be a list with 100 integers and the second argument must be a float between 1 and 100. The list represents the $$y$$-values which match the $$x$$-values $$1, 2, \ldots, 100$$. The function returns the $$y$$-value which corresponds with the $$x$$-value given by the second argument. If the arguments do not meet the right conditions, an error message must be printed and the value None must be returned. Look at the example below to understand these error messages.

Example

>>> linearInterpolation(list(range(1, 101)), 10.75)
10.75
>>> linearInterpolation(list(range(1, 101))[::-1], 10.75)
90.25
>>> linearInterpolation([42] * 100, 10.75)
42.0
>>> linearInterpolation(42, 10.75)
Expected type: <class 'list'>, Received type: <class 'int'>
>>> linearInterpolation(42, 0)
Expected type: <class 'list'>, Received type: <class 'int'>
>>> linearInterpolation([42], 10)
Expected type: <class 'float'>, Received type: <class 'int'>
>>> linearInterpolation([42], 10.75)
Expected length: 100, Received length: 1
>>> linearInterpolation([42] * 100, 100.75)
Interpolation is only possible for the values 1 up to and including 100.