The sestina is an unusual form of poetry that must comply to very stringent rules. Each sestina has six stanzas that use the same six line-ending words, rotated according to a set pattern:

A sestina may end in an envoi: a seventh three-line stanza. This intriguingly insistent form has appealed to verse writers since the 12th century. John Frederick Nims describes it in the following way:
In a good sestina the poet has six words, six images, six ideas so urgently in his mind that he cannot get away from them. He wants to test them in all possible combinations and come to a conclusion about their relationship.
The oldest-known sestina is Lo ferm voler qu'el cor m'intra written around 1200 by Arnaut Daniel, a troubadour of Aquitanian origin. He refers to it using the Occitan term cledisat, meaning, more or less, interlock. Hence, Daniel is generally considered the form's inventor, though it has been suggested that he may only have innovated an already existing form.

Assignment
The number six plays a key role in the rules defining a sestina. In this assignment you are asked to check whether or not a given poem — whose lines are stored in a text file — complies to a set of very stringent rules that resemble those of the sestina. However, we will not fixes the rules to the number six, but formulate them more generally in terms of the integer $$n \in \mathbb{N}_0$$. Before we come to a listing of the rules, we must first be clear about some basic concepts.
A poem consists of a sequence of stanzas that each consist of a sequence of lines, with stanzas separated from each other by at least one empty line. An empty line is a line that only contains whitespace characters (spaces, tabs and/or newlines). Empty lines may also occur before the first stanza and after the last stanza of the poem. The words of a poem are defined as the longest possible sequence of letters. Each line in a stanza contains at least one word, and the last word of the line is called its endword.
A permutation of a sequence of $$n$$ elements is a sequence of $$n$$ elements that results from rearranging the elements of the original sequence. A permutation is represented by a list containing the integers 1 up to $$n$$, in a random order. For example, the list [6, 1, 5, 2, 4, 3] represents the permutation that has the sixth element in the original sequence as its first element, followed by the first, fifth, second, forth and third elements of the original sequence.
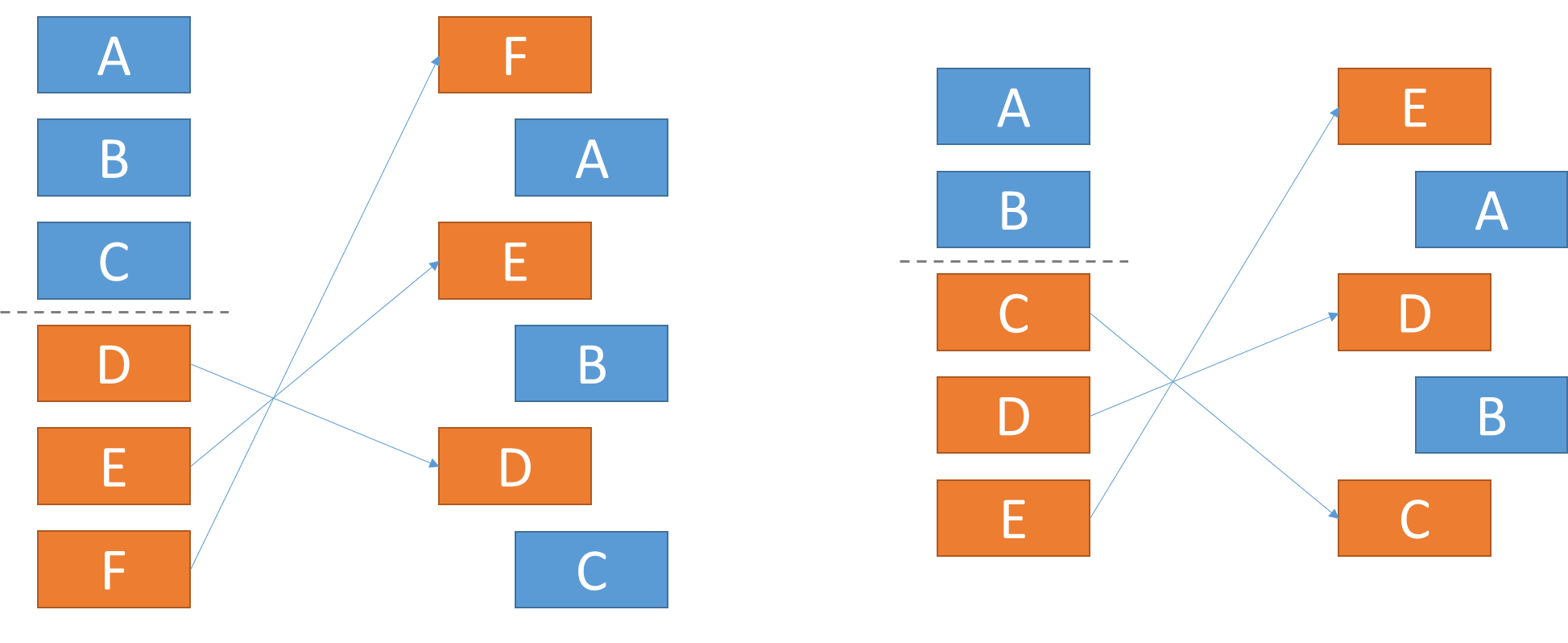
The canonical permutation of a sequence of $$n$$ elements is determined using the following procedure. Split the $$n$$ elements into two halves. In case $$n$$ is odd, the second half has one additional element compared to the first half. Reverse the order of the elements in the second half, and have each of those elements followed by the next element in the first half. The scheme below illustrates this procedure for an even (left) and odd (right) number of elements. This canonical permutation is the default permutation used to determine the order of the endwords in a sestina (for $$n = 6$$) and a pentina (for $$n = 5$$).
For a given poem we determine $$n \in \mathbb{N}_0$$ as the number of lines in its first stanza. The rules to which a sestina-like poem has to comply are:
the poem has $$n$$ stanzas that each have $$n$$ lines, possibly followed by an additional stanza (the envoi) that has $$\lfloor \frac{n}{2} \rfloor$$ lines; the notation $$\left \lfloor{x}\right \rfloor \in \mathbb{N}$$ denotes the integer part of $$x \in \mathbb{R}^{+}$$
applying a given permutation on the sequence of endwords of the first $$n - 1$$ stanzas each time results in the sequence of endwords of the next stanza; comparison between endwords must be case insensitive
the endwords of the envoi (if present) are also used as endwords in the other stanzas; comparison between endwords must be case insensitive; we want to stress that in contrast to the first $$n$$ stanzas, there are no restrictions on the order of the endwords of the envoi
You must proceed as follows to check whether or not a given poem complies to the above rules:
Write a function endword that takes a string as its argument. The function may assume that the given string has at least one word and must return its endword.
Write a function stanzas that takes the location of a text file containing the lines of a poem. The function must return a list containing the sequence of stanzas in the poem. Each stanza must itself be represented as a list containing the endwords of its lines. All endwords must be converted into lowercase letters.
Write a function permutation that takes a list of $$n \in \mathbb{N}_0$$ elements. The function also has a second optional parameter pattern that may take a list of numbers that should represent a permutation of a sequence of $$n$$ elements. The function must return a new list the contains the given permutation of the elements in the given list. If the value passed to the parameter pattern does not represent a rearrangement of the integers 1 up to and including $$n$$, the function must raise an AssertionError with the message invalid permutation. If no value was explicitly passed to the parameter pattern, the function must return the canonical permutation of the given list of elements.
Write a function sestina that takes the location of a text file containing the lines of a poem. The function also has a second optional parameter pattern that has the same meaning as with the function permutation. The function must return a Boolean value that indicates wheter or not the given poem complies to all rules for sestina-like poems as given above. In checking the second rule, the function must of course make use of the permutation that is described by the argument passed to the parameter pattern.
Example
The following interactive session assumes that the text files sestina0.txt1, sestina1.txt2 and sestina2.txt3 are located in the current directory.
>>> endword("Lo ferm voler qu'el cor m'intra")
'intra'
>>> endword("no'm pot ges becs escoissendre ni ongla")
'ongla'
>>> endword("de lauzengier qui pert per mal dir s'arma;")
'arma'
>>> stanzas('sestina0.txt')
[['intra', 'ongla', 'arma', 'verja', 'oncle', 'cambra'], ['cambra', 'intra', 'oncle', 'ongla', 'verja', 'arma'], ['arma', 'cambra', 'verja', 'intra', 'ongla', 'oncle'], ['oncle', 'arma', 'ongla', 'cambra', 'intra', 'verja'], ['verja', 'oncle', 'intra', 'arma', 'cambra', 'ongla'], ['ongla', 'verja', 'cambra', 'oncle', 'arma', 'intra'], ['oncle', 'arma', 'intra']]
>>> stanzas('sestina1.txt')
[['enters', 'nail', 'soul', 'rod', 'uncle', 'room'], ['room', 'enters', 'uncle', 'nail', 'rod', 'soul'], ['soul', 'room', 'rod', 'enters', 'nail', 'uncle'], ['uncle', 'soul', 'nail', 'room', 'enters', 'rod'], ['rod', 'uncle', 'enters', 'soul', 'room', 'nail'], ['nail', 'rod', 'room', 'uncle', 'soul', 'enters'], ['nail', 'soul', 'enters']]
>>> stanzas('sestina2.txt')
[['woe', 'sound', 'cryes', 'part', 'sleepe', 'augment'], ['augment', 'woe', 'sound', 'cryes', 'part', 'sleepe'], ['sleepe', 'augment', 'woe', 'sound', 'cryes', 'part'], ['part', 'sleepe', 'augment', 'woe', 'sound', 'cryes'], ['cryes', 'part', 'sleepe', 'augment', 'woe', 'sound'], ['sound', 'cryes', 'part', 'sleepe', 'augment', 'woe'], ['sound', 'part', 'augment']]
>>> permutation(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'])
['woe', 'rose', 'rhyme', 'love', 'sang', 'heart']
>>> permutation(['woe', 'rose', 'rhyme', 'love', 'sang', 'heart'])
['heart', 'woe', 'sang', 'rose', 'love', 'rhyme']
>>> permutation(['rose', 'love', 'heart', 'sang', 'rhyme'])
['rhyme', 'rose', 'sang', 'love', 'heart']
>>> permutation(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'], [6, 1, 5, 2, 4, 3])
['woe', 'rose', 'rhyme', 'love', 'sang', 'heart']
>>> permutation(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'], [6, 5, 4, 3, 2, 1])
['woe', 'rhyme', 'sang', 'heart', 'love', 'rose']
>>> permutation(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'], [6, 1, 5, 3, 4, 3])
Traceback (most recent call last):
AssertionError: invalid permutation
>>> sestina('sestina0.txt')
True
>>> sestina('sestina0.txt', [6, 1, 5, 2, 4, 3])
True
>>> sestina('sestina1.txt')
True
>>> sestina('sestina2.txt')
False
>>> sestina('sestina2.txt', [6, 1, 2, 3, 4, 5])
True