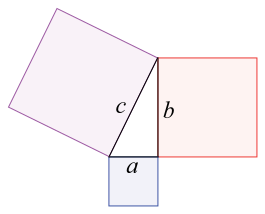
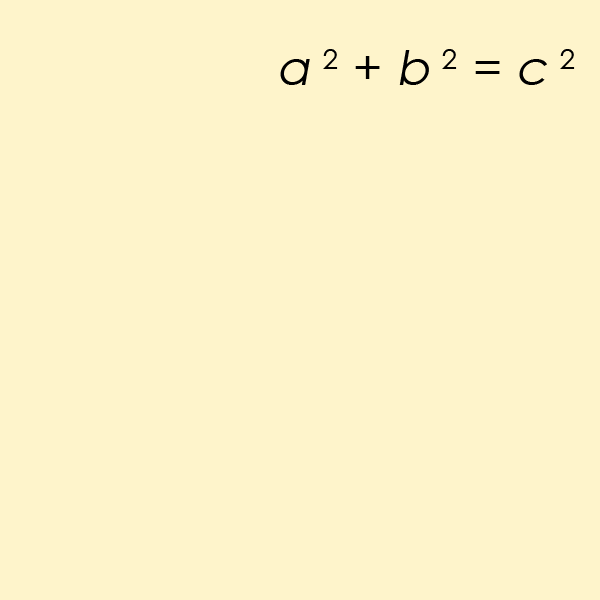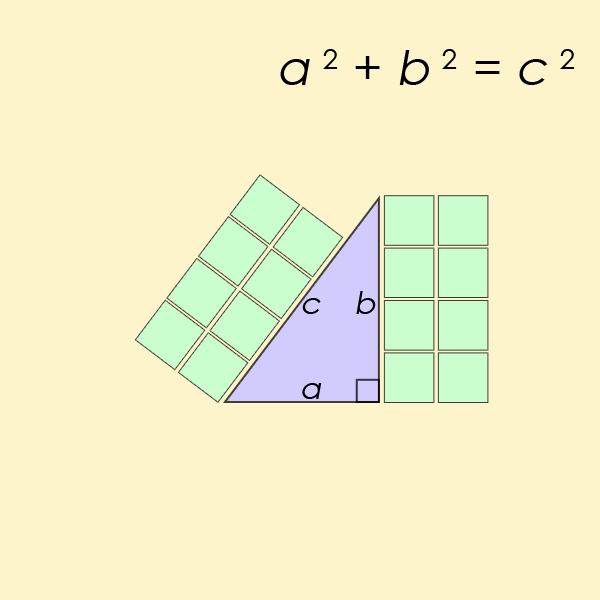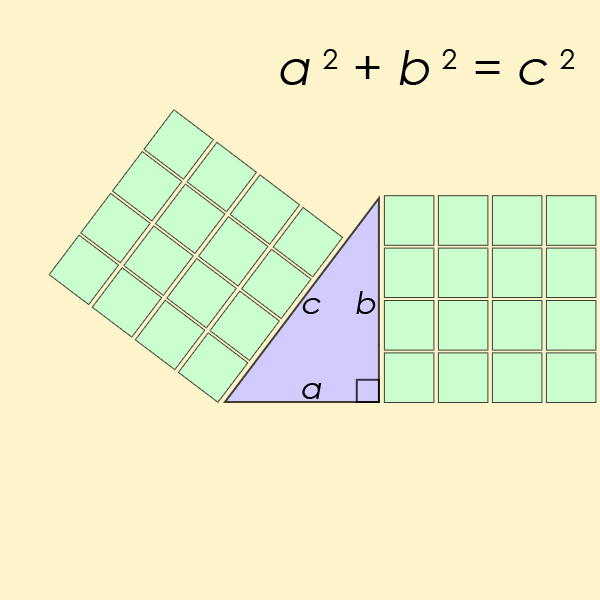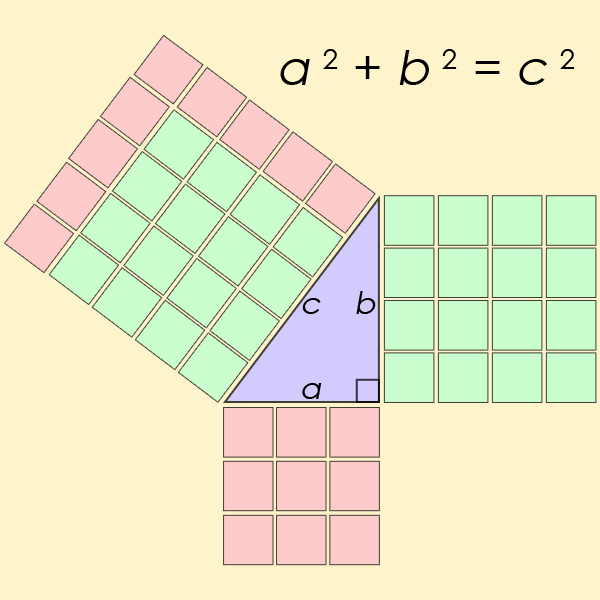A Pythagorean triple1 $$(a, b, c)$$ consists of three strictly positive integers $$a$$, $$b$$ and $$c$$, for which \[ a^2 + b^2 = c^2 \] The name is derived from the Pythagorean theorem2, stating that every right triangle has side lengths satisfying the formula $$a^2 + b^2 = c^2$$. Thus, Pythagorean triples describe the three integer side lengths of a right triangle. However, right triangles with non-integer sides do not form Pythagorean triples.
A well-known example of a Pythagorean triple is $$(3, 4, 5)$$, but also its multiples such as $$(6, 8, 10)$$ and $$(9, 12, 15)$$ are Pythagorean triples. In general, if $$(a, b, c)$$ is a Pythagorean triple, then so is $$(ka, kb, kc)$$ for any positive integer $$k$$. A primitive Pythagorean triple $$(a, b, c)$$ is one in which $$a$$, $$b$$ and $$c$$ are coprime3. As an example, there are four Pythagorean triples $$(a, b, c)$$ for which $$a + b + c = 240$$: $$(15, 112, 113)$$, $$(40, 96, 104)$$, $$(48, 90, 102)$$ and $$(60, 80, 100)$$.
Pythagorean triples have been known since ancient times. Babylonian clay tablets dating from the time of Hammurabi4 already mention Pythagorean triples. The oldest known record comes from Plimpton 3225, a Babylonian clay tablet from about 1800BC, written in a sexagesimal6 number system. It was discovered by Edgar James Banks7 shortly after 1900, and sold to George Arthur Plimpton8 in 1922 for $10. This clay tablet lists 15 triplets, including $$(56, 90, 106)$$, $$(119, 120, 169)$$ and even $$(12709, 13500, 18541)$$. Pythagorean triples were also known in India. The earliest Baudhayana-Sulbasutra9 (dating back to the sixth century before Christ) contains five such triples.
Input
A number $$n \in \mathbb{N}_0$$.
Output
A list of all Pythagorean triples $$(a, b, c)$$ for which $$0 < a \leq b \leq c$$ and $$a + b + c = n$$. These triples must be written as (a, b, c), each on a separate line and sorted in increasing order according to $$a$$, then $$b$$ and then $$c$$.
Example
Input:
240Output:
(15, 112, 113)
(40, 96, 104)
(48, 90, 102)
(60, 80, 100)