At the beginning of our era, the Maya settled in Central America. In many ways, they were by far the most developed and fascinating civilization of their age. They didn't know wheels or draught animals, but they controlled the art of weaving, architecture and pottery-making like no other. But it was their realizations in mathematics and astronomy that were truly breath-taking. While Europe was trying to get through the dark Middle Ages, the Maya calculated the solar year to 365,242 days (which, according to the modern calculations is 365,242198 days) and the moon cycle to 29,5302 days (29,53059 days according to modern calculations). Such staggering calculations could barely have been possible if it weren't for the powerful scale the Maya used.
Maya priests and astronomers used a scale with base 20. In that scale, the numbers (0-19) were presented by means of three symbols: zero (form of a shell), one (a dot) and five (a horizontal line). Nineteen (19), for example, is written as four dots that are horizontally next to each other, on top of three horizontal lines that are placed on top of each other. The concepts 'digit' and 'zero' were quite unusual for that time, and completely unknown in Europe.
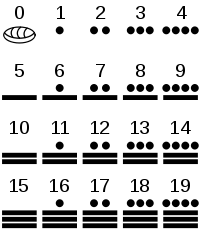
For Maya numbers consisting of multiple Maya digits— so numbers with a value large than 19 — the Maya numbers are written on top of each other. Here, the number with the highest value is on top. The number thirty-three, for example, is written as a dot (upper Maya number), with three dots underneath, on top of 2 horizontal lines (lower Maya number). The first dot represents "one twenty" or $$1 \times 20$$, to which three dots and two horizontal lines (13) are added. Consequentially, you get $$(1 \times 20) + 13 = 33$$. Oddly enough, in the Maya scale the digit in the third position (counted from bottom to top) does not have $$20 \times 20 = 400$$ as a value, but $$18 \times 20 = 360$$. Supposedly because 360 is about equal to the number of days in a calendar year. All Maya numbers above the third position (counted from the bottom) again have a normal value according to the 20 digit scale, that makes $$360 \times 20 = 7200$$ for the fourth digit, $$7200 \times 20 = 144000$$ for the fifth digit, and so on. This way, the table underneath indicates that $$12 \times 360 + 16 \times 20 + 5 = 4645$$ and that $$9 \times 7200 + 5 \times 360 + 13 \times 20 + 16 = 66876$$.
| unit | 33 | 389 | 4645 | 66876 |
|---|---|---|---|---|
| 7200 |
|
|||
| 360 |
|
|
|
|
| 20 |
|
|
|
|
| 1 |
|
|
|
|
Assignment
For this assignment, Maya numbers and Maya digits are represented as strings. The Maya digits with value zero are noted with the letter S, and other digits as a sequence of dots (.; value 1) and hyphens (-; value 5). Here, the dots are always in front of the hyphens. The Maya digits of a Maya number are written next to each other from left to right — separated by a space — instead of on to top of each other. This way, the Maya number with value 66876 is represented as the string "....- - ...-- .---". You are asked to write a function maya2deci that prints the decimal value of a given Maya number. The string representation of this number has to be given to the function as an argument.
Example
>>> maya2deci('..')
2
>>> maya2deci('. ...--')
33
>>> maya2deci('. . ....-')
389
>>> maya2deci('..-- .--- -')
4645
>>> maya2deci('. ..--- ...- ---')
13495
>>> maya2deci('....- - ...-- .---')
66876
>>> maya2deci('...- .-- S S S')
1231200