Most jigsaw puzzles can only be solved once and then you're done. But the Daily Calendar Puzzle is a very fun and addictive puzzle that each day provides a new challenge. All you have to do is put the ten puzzle pieces in the calendar frame so that the three uncovered squares are labeled with a weekday, a day and a month.

It would be a lie to say that all date are easy to form, but there is at least one solution for every day. Can you make today's date? Your birthday? A historical event?

Assignment

The calendar frame of a Daily Calendar Puzzle consists of a $$8 \times 7$$ grid with 8 rows and 7 columns. Each of the 56 squares in the grid is assigned a number from 0 to 55 (int) by going through the grid from left to right and from top to bottom. Six squares cannot be covered by puzzle pieces: 6, 13, 49, 50, 51 and 52 (marked with a darker background color in the image below). All other squares have a unique label: in order by increasing number the English three-letter abbreviations for the twelve months of the year (Jan–Dec), the day numbers (1–31) and the English three-letter abbreviations for the seven weekdays (Sun–Sat).

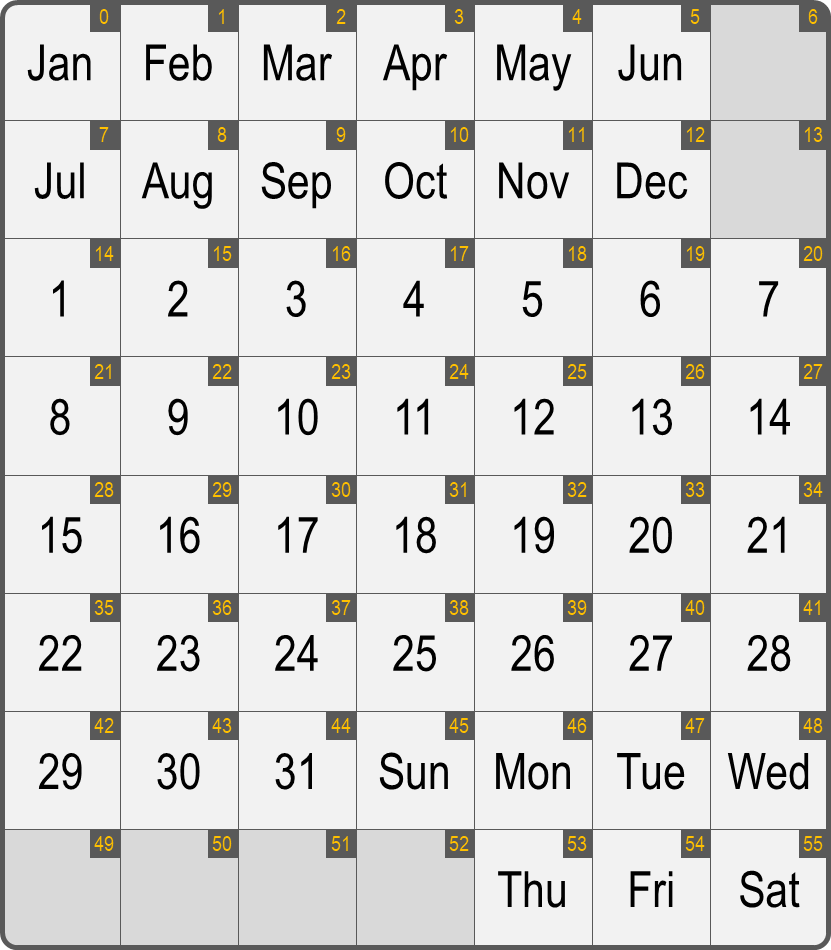
Each puzzle piece is assigned a unique uppercase letter (str) as a label to distinguish it from other pieces. We represent the place where a piece is put down in the frame as a collection (list, tuple or set) with the numbers of the squares covered by the piece. At the same time, this also describes the shape of the piece. Here we have put down, for example, a straight orange puzzle piece in place (0, 1, 2, 3), covering the four squares on the left side of the top row.

Define a class Calendar to represent frames of a Daily Calendar Puzzle in which puzzle pieces may be put down and removed. No arguments must be passed when creating a new frame (Calendar): each frame has the same dimensions and no puzzle pieces have been put down in the frame initially. A frame $$f$$ (Calendar) must at least support the following methods:

A method square that takes the number $$n$$ (int) of a square. The method must return a string representation (str) of square $$n$$ consisting of three characters:
- ###: if no puzzle pieces can be placed on square $$n$$
- #?#: if square $$n$$ is covered by a puzzle piece in frame $$f$$, with the label of that piece at the question mark
- ???: if square $$n$$ is not covered by a puzzle piece in frame $$f$$, with the label of square $$n$$ at the three questions marks; labels containing less than three characters are left padded with spaces; the English three-letter abbreviations for the twelve months are
  
  Jan,Feb,Mar,Apr,May,Jun,Jul,Aug,Sep,Oct,Nov,Dec
  
  and the English three-letter abbreviations for the seven weekdays are
  
  Sun,Mon,Tue,Wed,Thu,Fri,Sat
A method piece that takes the label $$l$$ of a puzzle piece. If no piece with label $$l$$ has been put down in frame $$f$$, an AssertionError must be raised with message no piece ? in the frame, where label $$l$$ comes at the question mark. Otherwise, the method must return a set (set) containing the numbers of all squares that are covered by the piece with label $$l$$ in frame $$f$$.
A method put that takes the label $$l$$ and the place $$p$$ of a puzzle piece. If a piece with label $$l$$ has already been put down in frame $$f$$, an AssertionError must be raised with message piece ? already in the frame. If the piece can not be put down at place $$p$$ in frame $$f$$, an AssertionError must be raised with message can't put piece ? in the frame. In both cases, label $$l$$ comes at the question mark. Otherwise, frame $$f$$ must keep track that a piece with label $$l$$ has been put down at place $$p$$ and the method must return a reference to frame $$f$$.
A method remove that takes the label $$l$$ of a puzzle piece. If no piece with label $$l$$ has been put down in frame $$f$$, an AssertionError must be raised with message no piece ? in the frame, where label $$l$$ comes at the question mark. Otherwise, the piece with label $$l$$ must be removed from frame $$f$$ and the method must return a reference to frame $$f$$.
A method read that takes no arguments. If there are three squares in frame $$f$$ that are not covered by a puzzle piece and are labeled respectively with a weekday $$w$$, a day number $$d$$ and a month $$m$$, a string must be returned with weekday $$m$$ followed by a comma, a space, day number$$d$$ (without leading spaces), another space and month $$m$$. Otherwise, an AssertionError must be raised with message invalid date.

If a frame $$f$$ (Calendar) is passed to the built-in function str, a string representation (str) of the frame must be returned. Each row of the frame is a separate line in the string representation, listing the string representations of the squares on that row from left to right, separated by spaces.

Example

        >>> frame = Calendar()
>>> frame.square(0)
'Jan'
>>> frame.square(39)
' 26'
>>> frame.square(48)
'Wed'
>>> frame.square(52)
'###'
>>> print(frame)
Jan Feb Mar Apr May Jun ###
Jul Aug Sep Oct Nov Dec ###
  1   2   3   4   5   6   7
  8   9  10  11  12  13  14
 15  16  17  18  19  20  21
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> frame.piece('A')
Traceback (most recent call last):
AssertionError: no piece A in the frame
>>> print(frame.put('A', (0, 1, 2, 3)))
#A# #A# #A# #A# May Jun ###
Jul Aug Sep Oct Nov Dec ###
  1   2   3   4   5   6   7
  8   9  10  11  12  13  14
 15  16  17  18  19  20  21
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> frame.piece('A')
{0, 1, 2, 3}
>>> print(frame.put('B', (4, 5, 9, 10, 11)))
#A# #A# #A# #A# #B# #B# ###
Jul Aug #B# #B# #B# Dec ###
  1   2   3   4   5   6   7
  8   9  10  11  12  13  14
 15  16  17  18  19  20  21
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> frame.put('B', (7, 8, 14, 21, 28))
Traceback (most recent call last):
AssertionError: piece B already in the frame
>>> frame.put('C', (13, 14, 15))
Traceback (most recent call last):
AssertionError: can't put piece C in the frame
>>> frame.put('C', (0, 1, 7, 8))
Traceback (most recent call last):
AssertionError: can't put piece C in the frame
>>> print(frame.put('C', [7, 8, 14, 21, 28]).put('D', [15, 16, 22, 23, 29]))
#A# #A# #A# #A# #B# #B# ###
#C# #C# #B# #B# #B# Dec ###
#C# #D# #D#   4   5   6   7
#C# #D# #D#  11  12  13  14
#C# #D#  17  18  19  20  21
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> print(frame.remove('A'))
Jan Feb Mar Apr #B# #B# ###
#C# #C# #B# #B# #B# Dec ###
#C# #D# #D#   4   5   6   7
#C# #D# #D#  11  12  13  14
#C# #D#  17  18  19  20  21
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> frame.remove('Z')
Traceback (most recent call last):
AssertionError: no piece Z in the frame
>>> print(frame.put('A', (0, 1, 2, 3)))
#A# #A# #A# #A# #B# #B# ###
#C# #C# #B# #B# #B# Dec ###
#C# #D# #D#   4   5   6   7
#C# #D# #D#  11  12  13  14
#C# #D#  17  18  19  20  21
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> print(frame.put('E', {17, 24, 25, 26, 33}).put('F', {18, 19, 20, 27, 34}))
#A# #A# #A# #A# #B# #B# ###
#C# #C# #B# #B# #B# Dec ###
#C# #D# #D# #E# #F# #F# #F#
#C# #D# #D# #E# #E# #E# #F#
#C# #D#  17  18  19 #E# #F#
 22  23  24  25  26  27  28
 29  30  31 Sun Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> print(frame.put('G', (30, 31, 32, 38, 45)).put('H', (35, 36, 37, 42, 44)))
#A# #A# #A# #A# #B# #B# ###
#C# #C# #B# #B# #B# Dec ###
#C# #D# #D# #E# #F# #F# #F#
#C# #D# #D# #E# #E# #E# #F#
#C# #D# #G# #G# #G# #E# #F#
#H# #H# #H# #G#  26  27  28
#H#  30 #H# #G# Mon Tue Wed
### ### ### ### Thu Fri Sat
>>> frame.read()
Traceback (most recent call last):
AssertionError: invalid date
>>> print(frame.put('I', (39, 40, 41, 48)).put('J', (46, 47, 54, 55)))
#A# #A# #A# #A# #B# #B# ###
#C# #C# #B# #B# #B# Dec ###
#C# #D# #D# #E# #F# #F# #F#
#C# #D# #D# #E# #E# #E# #F#
#C# #D# #G# #G# #G# #E# #F#
#H# #H# #H# #G# #I# #I# #I#
#H#  30 #H# #G# #J# #J# #I#
### ### ### ### Thu #J# #J#
>>> frame.read()
'Thu, 30 Dec'

Assignment

Example

Epilogue

Spoiler alert