There is chaos in the air traffic centers of all European airports. Eyjafjallajökull — an ice-covered strato-volcano in Iceland — has just erupted. The ash cloud caused by this volcanic eruption is spreading rapidly across the European continent. A closure of the airspace over much of northern Europe is imminent. Your task is to identify whether any other volcanoes are likely to erupt and to follow the ash clouds they cause very closely. Based on this information, you must advise if can still be organized between two given airports.

To maintain the overview, we have divided a map into square areas that form a rectangular grid. When a volcano erupts, we indicate this by drawing a cloud over the square where the volcano is situated. The spread of ash clouds is modeled by highlighting the squares that are at the top, at the bottom, on the left or on the right from the square that was already marked with a cloud in every following step. In order to keep things simple, we have numbered the columns in the example grid below in an increasing order from left to right and the rows from bottom to top. The order of the numbers has little importance for the rest of the exercise, as long as it is done with whole numbers in an increasing order. This way we can indicate a certain square with its column number and row number. The example shows how an ash cloud spreads over the adjacent squares after an eruption in square $$(0, 0)$$.

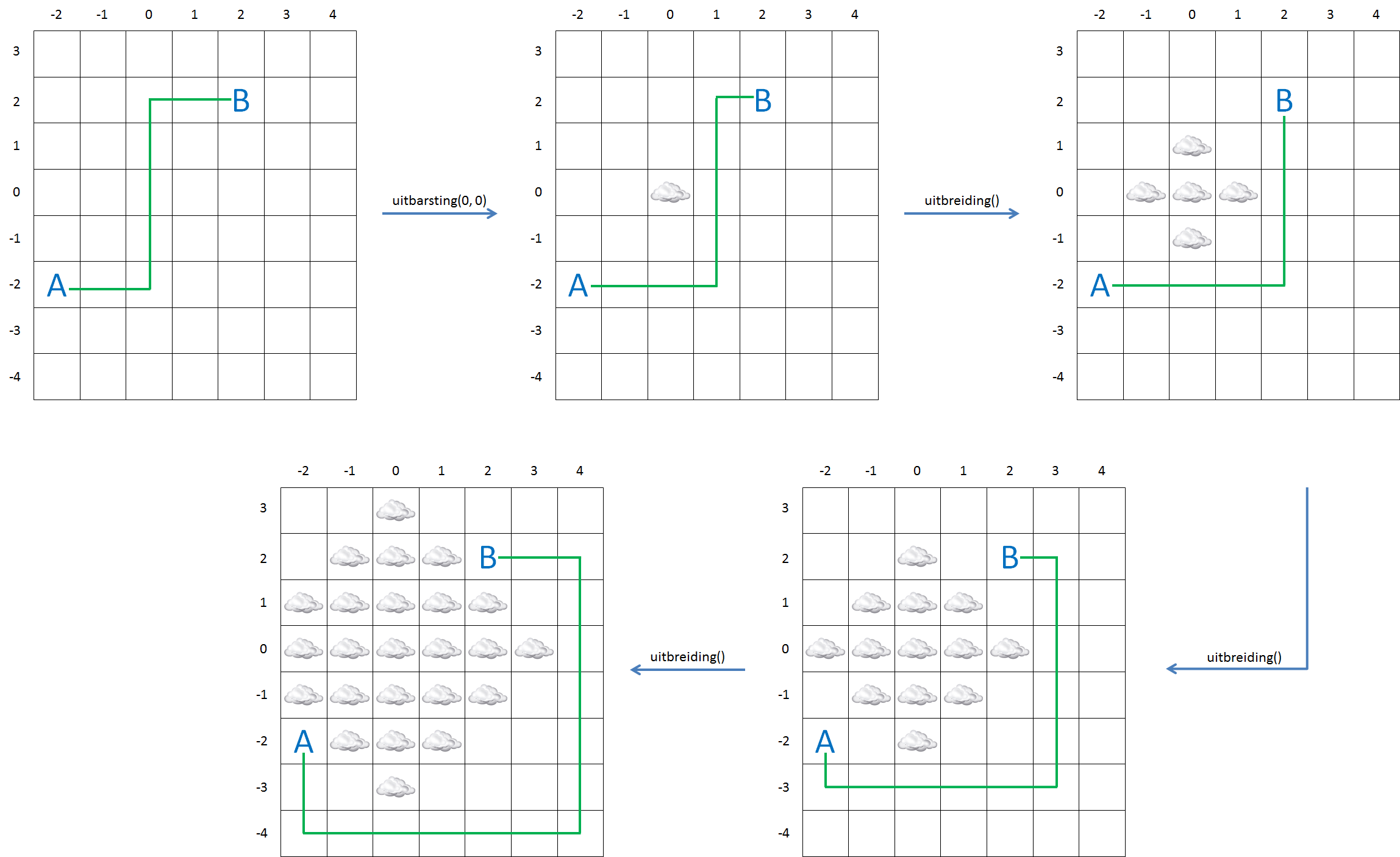
To advise whether any flights can be organized between two airports, you determine the distance of the shortest route from one airport to another without flying through the ash cloud. We will explain the procedure to determine this distance with the image below. The squares in which the airports are situated, are indicated with the letters A and B. A flying route can't go through any of the squares that are marked with clouds. 

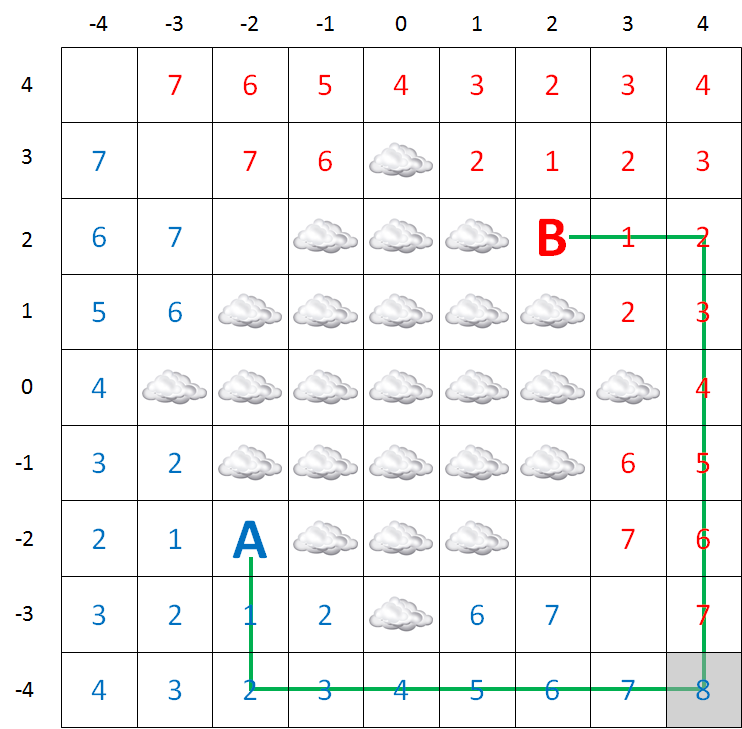
If one of the airports, or both of them, is situated in a square that is marked with a cloud, it is impossible to fly from that airports, otherwise, the shortest route cant be determined as follows:

1. mark the square A and B with the value 0 (zero)

2. equate $$i$$ with 0

3. mark every square that is above, below, left or right from A that is marked with a cloud, with value $$i$$ and give value $$i + 1$$ to every square that hasn't been marked yet; These markings are given in blue in the picture above.

4. mark every square that is above, below, left or right from B that is marked with a cloud, with value $$i$$ and give value $$i + 1$$ to every square that hasn't been marked yet; These markings are given in red in the picture above.

5. if no additional square can be numbered in step 3 or in step 4, both airports are completely isolated and no route can be found.

6. when there are two horizontally or vertically adjacent squares are marked one in blue and one in red in step 3 and 4, you have found the shortest route and the procedure ends.

7. raise $$i$$ with 1

8. return to 3

The only thing you have to think about yourself is how you will calculate the shortest distance that you have found in step 6. The distance of the route is expressed in the number of steps to adjacent squares (horizontally or vertically touching the current square). that you have to take to go from one airport to another. In the example above, the shortest route is 16.

Assignment

Define a class Map which can be used to follow the evolution of ash clouds over a rectangular square, an which can also be used to determine the shortest route — that doesn't go through an ash cloud — to get from one airport to another. The objects of this class must contain at least the following properties and methods. 

• Every object of the class Map must have the property ashcloud, that refers to a collection. When making a new object, this collection is empty, but the two following methods are used to change the contents of the collection.

• A method eruption to which two whole numbers must be given, these numbers respectively indicate the column number $$k$$ and the row number $$r$$of a square in the grid in which the eruption takes place. The fact that this eruption causes an ash cloud, is saved by adding the tuple $$(k, r)$$ to the collection ash cloud.

• A method spread to which no arguments should be given. By calling this method, the co-ordinates of all squares that were added to the collection ash cloud, that touch the square that was already indicated with an ash cloud on the left, on the right, above or below.

• A method shortestRoute to which two tuples with the co-ordinates of the two airports must be given. The method must print the length of the shortest route between those airports, that does not go through the ash cloud. If one of both airports is situated beneath an ash cloud, or is both airports are completely isolated, the value -1 must be printed as a result.

Example

>>> airmap = Map()
>>> airmap.eruption(0, 0)
>>> airmap.ashcloud
{(0, 0)}
>>> airmap.spread()
>>> airmap.ashcloud
{(0, 1), (0, -1), (1, 0), (0, 0), (-1, 0)}
>>> airmap.shortestRoute((-2, -2), (2, 2))
8
>>> airmap.spread()
>>> airmap.ashcloud
{(0, 1), (-1, 1), (0, 0), (-1, 0), (-1, -1), (1, 1), (2, 0), (0, -2), (0, -1), (1, 0), (1, -1), (0, 2), (-2, 0)}
>>> airmap.shortestRoute((-2, -2), (2, 2))
12
>>> airmap.spread()
>>> airmap.shortestRoute((-2, -2), (2, 2))
16
>>> airmap.spread()
>>> airmap.shortestRoute((-2, -2), (2, 2))
-1