Make an inverted triangle (pointing downwards) of hexagonal cells.
Color the cells in the top row randomly in three colors: red, yellow and blue.
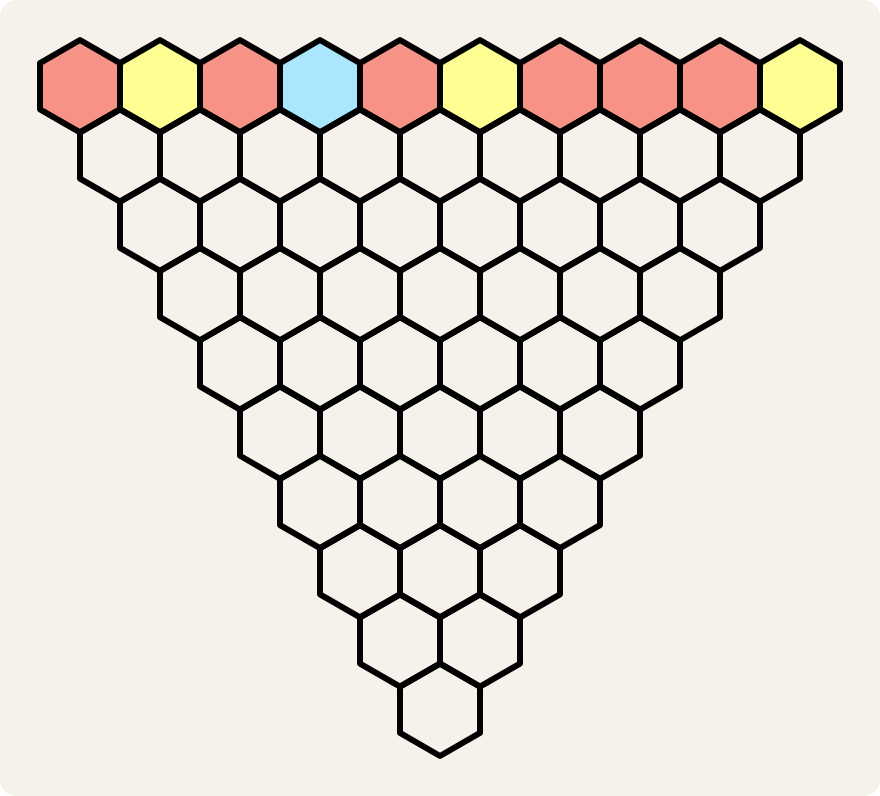
Now color the cells in the second row according to these rules:
-
if the two neighboring cells immediately above are of the same color, assign that color
-
if the two neighboring cells immediately above are of different colors, assign the third color
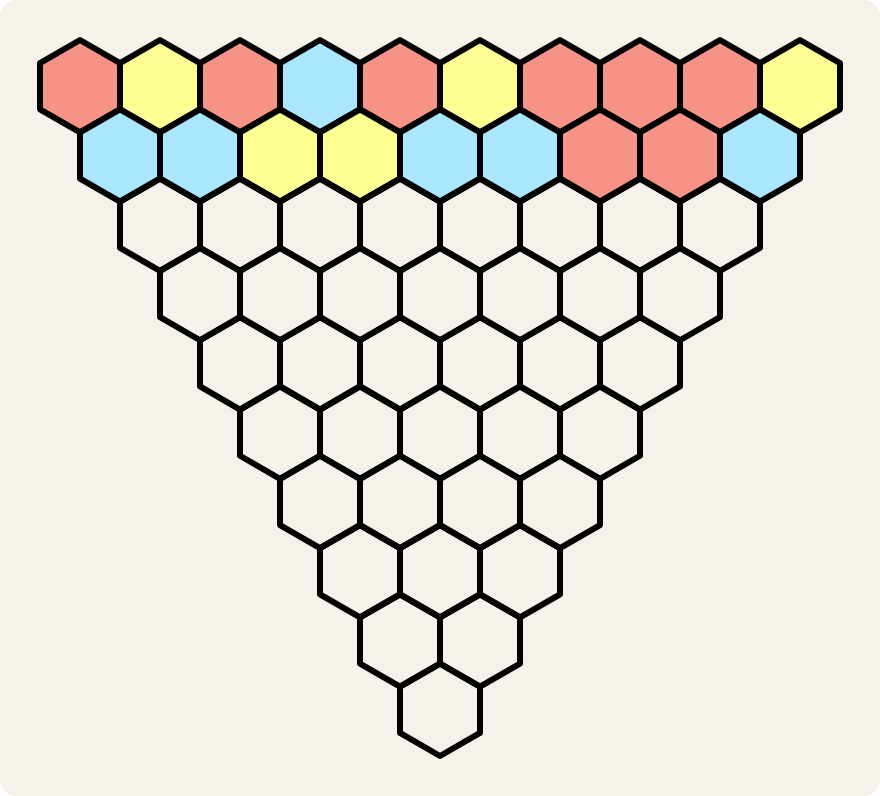
When you've finished the second row, continue through the succeeding ones, applying the same rules.
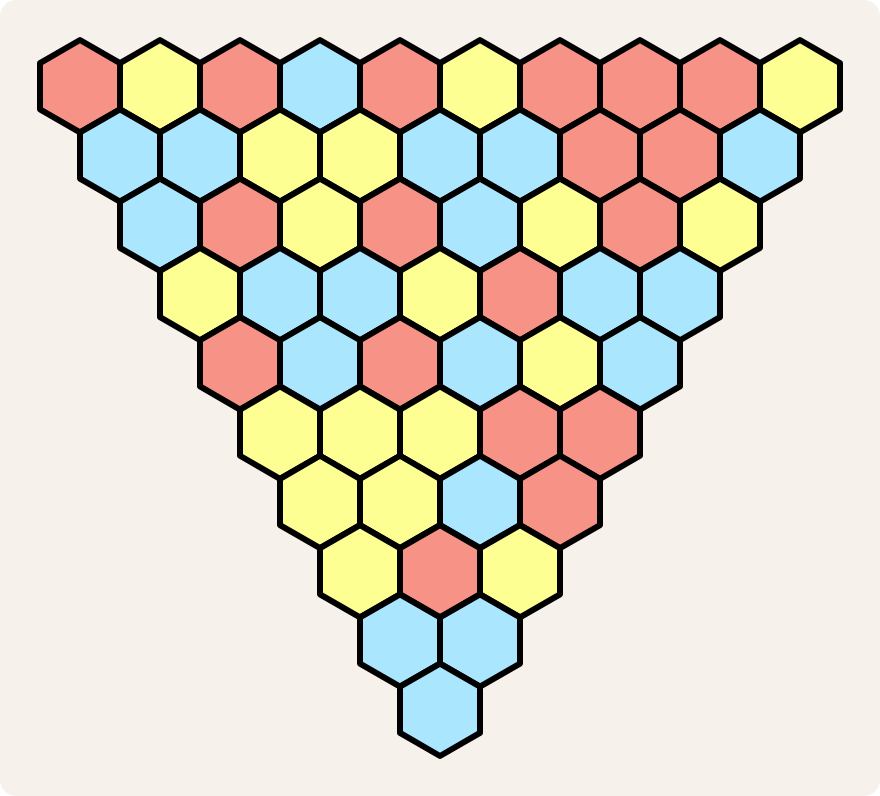
Pleasingly, if the top row of the triangle consists of $$3^n + 1$$ cells (2, 4, 10, 28, …), the color of the last cell can be predicted at the start: just apply our two rules to the outer cells of the top row. If those two cells are both red, the bottom cell will be red. If one is red and one is yellow (as in the example above), the bottom cell will be blue.
Assignment
We represent a colored cell as the character (str) depicting a square in the corresponding color: '🟨' (yellow), '🟥' (red) or '🟦' (blue).
Rendering of colored squares in PyCharm under MS Windows
In PyCharm under MS Windows, the characters depicting colored squares are rendered as monochrome squares with a different shading for each color. This makes the difference between the three characters a little more subtle, but otherwise they just remain three distinct characters.
We represent a row of colored cells as a string (str) containing the representations of the colored cells, listed from left to right.
We represent an inverted triangle of colored cells as a list of rows of colored cells (str), listed from top to bottom.
Your task:
-
Write a function color that takes the two colored cells (str) immediately neighboring above a third colored cell in an inverted triangle. The function must return that third colored cell (str), whose color is determined by applying our two rules.
-
Write a function bottom_color that takes a row of colored cells (str). The function must return the colored cell (str) obtained by applying our two rules to the outer cells of the given row of colored cells.
Note
Contrary to what the name bottom_color might suggest, the result of this function does not necessarily have to be a correct prediction for the color of the bottom cell of an inverted triangle whose cells in the top row are colored according to the pattern of the given row of colored cells. The prediction is only guaranteed to be correct if the top row consists of $$3^n + 1$$ cells. But your implementation of this function does not need to take that into account.
-
Write a function next_row that takes a row of colored cells (str). The function must return the next row of colored cells (str) in an inverted triangle, which is obtained by applying our two rules to the given row of colored cells.
-
Write a function tricolor_triangle that takes a row of colored cells (str). The function must return the inverted triangle (list) of colored cells, whose cells in the top row are colored according to the pattern of the given row of colored cells.
Example
>>> color('🟥', '🟥')
'🟥'
>>> color('🟨', '🟥')
'🟦'
>>> bottom_color('🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨')
'🟦'
>>> next_row('🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨')
'🟦🟦🟨🟨🟦🟦🟥🟥🟦'
>>> next_row('🟦🟦🟨🟨🟦🟦🟥🟥🟦')
'🟦🟥🟨🟥🟦🟨🟥🟨'
>>> tricolor_triangle('🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨')
['🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨', '🟦🟦🟨🟨🟦🟦🟥🟥🟦', '🟦🟥🟨🟥🟦🟨🟥🟨', '🟨🟦🟦🟨🟥🟦🟦', '🟥🟦🟥🟦🟨🟦', '🟨🟨🟨🟥🟥', '🟨🟨🟦🟥', '🟨🟥🟨', '🟦🟦', '🟦']
Epilogue
The principle was discovered in 2012 by Steve Humble, who teaches primary and second school trainee teachers in the education department at Newcastle University in northeastern England. Asked about the insight at the core of the principle, he responded:
As for the discovery it was just that — I wanted to discuss randomness with families, and created this color game to play. The idea was to show how order came from initial disorder. You get these patches of triangle color.
In working with this game I spotted that the top end two colors gave the bottom color. I ran some computer code and discovered not all cases worked but could not come up with a complete proof. I described the problem to Ehrhard Behrends in the summer at a conference in Murcia. In a few days he came back to me with a proof — and then we put together the paper. Ehrhard's genius was to generalize to $$n$$ colors and look at all the variety of ways we could set up the initial rules for creating the pattern.