There are $$n$$ people standing in a circle waiting to be executed. These people are numbered in clockwise order from 1 up to and including $$n$$. The counting out begins at person number 1, where each $$k$$-th person that is still alive is executed. The elimination proceeds clockwise around the circle (which is becoming smaller and smaller as the executed people are removed), until only the last person remains, who is given freedom. Can you choose the place in the initial circle so that you are the last one remaining and so survive?

The problem is named after Flavius Josephus¹, a Jewish historian living in the 1st century. According to Josephus' account of the siege of Yodfat, he and his 40 soldiers were trapped in a cave, the exit of which was blocked by Romans. They chose suicide over capture and decided that they would form a circle and start killing themselves using a step of three. Josephus states that by luck or maybe by the hand of God (some historians point out that Josephus was an extremely well-educated man, who might have quickly computed the outcome of the execution), he and another man remained the last and gave up to the Romans.

The reference comes from Book 3, Chapter 8, par 7 of Josephus' The Jewish War², writing of himself in the third person (translation from Hebrew to English by William Whiston):

However, in this extreme distress, he was not destitute of his usual sagacity; but trusting himself to the providence of God, he put his life into hazard [in the manner following]: "And now," said he, "since it is resolved among you that you will die, come on, let us commit our mutual deaths to determination by lot. He whom the lot falls to first, let him be killed by him that hath the second lot, and thus fortune shall make its progress through us all; nor shall any of us perish by his own right hand, for it would be unfair if, when the rest are gone, somebody should repent and save himself." This proposal appeared to them to be very just; and when he had prevailed with them to determine this matter by lots, he drew one of the lots for himself also. He who had the first lot laid his neck bare to him that had the next, as supposing that the general would die among them immediately; for they thought death, if Josephus might but die with them, was sweeter than life; yet was he with another left to the last, whether we must say it happened so by chance, or whether by the providence of God. And as he was very desirous neither to be condemned by the lot, nor, if he had been left to the last, to imbrue his right hand in the blood of his countrymen, he persuaded him to trust his fidelity to him, and to live as well as himself.

Assignment

Write a function

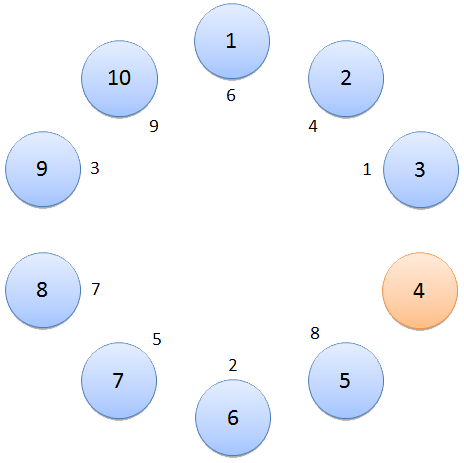
def josephus(n, k):

that may help Josephus to determine the right position in the circle. Two arguments must be passed to the function: the number of people $$n \in \mathbb{N}$$ ($$2 \leq n \leq 1.000$$) in the circle and an integer $$k \in \mathbb{N}$$ ($$2 \leq k \leq 1.000$$) that indicates after how many living persons someone gets executed. The function must return the position of the last person surviving the execution. As such, for a circle with 10 people where every third person gets executed, the function should return position 4. This outcome is illustrated in the animation below. Here, the circles contain the numbering of the people. The number outside a circle indicates the order in which the people get executed. If you proceed this way through the circle, person 4 survives at the end.

Example

>>> josephus(12, 3)
10
>>> josephus(41, 3)
31
>>> josephus(30, 9)
21