Kwadratensommen en Anova-tabel

In deze sectie bespreken we de constructie van kwadratensommen die typisch in een tabel worden gegeven en die behoren tot de klassieke presentatiewijze van een regressie-analyse. De tabel wordt de variantie-analyse tabel of anova tabel genoemd.

De totale kwadratensom is gelijk aan

\[\text{SSTot} = \sum_{i=1}^n (Y_i-\bar{Y})^2.\]

Het is de som van de kwadratische afwijkingen van de observaties rond het steekproefgemiddelde \(\bar Y\). Deze kwadratensom kan worden gebruikt om de variantie te schatten van de marginale distributie van de uitkomsten.

In dit hoofdstuk wordt de focus hoofdzakelijk gelegd op de conditionele distributie van \(Y\vert X=x\).
- We weten reeds dat MSE een schatter is van de variantie van de conditionele distributie van \(Y\vert X=x\).
- De marginale distributie van \(Y\) is de verdeling van \(Y\) wanneer we geen rekening houden met de waarde voor de predictor \(X\). Het heeft als gemiddelde \(E[Y]\) wat geschat wordt door het steekproefgemiddelde \(\bar{Y}\) en een variantie \(\text{var}[Y]\) die geschat kan worden aan de hand van \(\frac{\text{SSTot}}{n-1}\), de steekproefvariantie van \(Y\) (zie Sectie 4.3.2).

Een grafische interpretatie van SSTot wordt weergegeven in Figuur 37.

brca %>%
  ggplot(aes(y = log2S100A8, x = log2ESR1)) +
  geom_point(color = "blue") +
  geom_hline(aes(yintercept = mean(log2S100A8))) +
  geom_segment(aes(x = log2ESR1, xend = log2ESR1, y=log2S100A8,
                   yend =mean(log2S100A8)), lty = 2, color = "blue") +
  xlab("ESR1 expressie (log2)") +
  ylab("S100A8 expressie (log2)")

Figuur 36: Interpretatie van de totale kwadratensom (SSTot): de som van de kwadratische afwijkingen rond het steekproefgemiddelde.

Daarnaast kunnen we eveneens een tweede kwadratensom definiëren: de kwadratensom van de regressie, SSR, die een maat is voor de variabiliteit die verklaard kan worden door de regressie. Het is de som van de kwadratische afwijkingen van de voorspelde response \(\hat{Y}_i\) rond het steekproefgemiddelde \(\bar Y\).

De kwadratensom van de regressie is gelijk aan

\[\text{SSR} = \sum_{i=1}^n (\hat{Y}_i - \bar{Y})^2 = \sum_{i=1}^n (\hat{g}(x_i) - \bar{Y})^2.\]

SSR is een maat voor de afwijking tussen de predicties op de geschatte regressierechte en het steekproefgemiddelde van de uitkomsten. Het kan ook geïnterpreteerd worden als een maat voor de afwijking tussen de geschatte regressierechte \(\hat{g}(x)=\hat\beta_0+\hat\beta_1x\) en een “geschatte regressierechte” waarbij de regressor geen effect heeft op de gemiddelde uitkomst. Deze laatste is dus eigenlijk een schatting van de regressierechte \(g(x)=\beta_0\), waarin \(\beta_0\) geschat wordt door \(\bar{Y}\). Anders geformuleerd: SSR meet de grootte van het regressie-effect zodat \(\text{SSR} \approx 0\) duidt op geen effect van de regressor en \(\text{SSR}>0\) duidt op een effect van de regressor. We voelen reeds aan dat \(\text{SSR}\) zal kunnen worden gebruikt voor het ontwikkelen van een statistische test die de associatie tussen \(X\) en \(Y\) evalueert.

Een grafische interpretatie van SSR wordt weergegeven in Figuur 37.

lm2_df <- data.frame(log2S100A8 = brca$log2S100A8, fitted = lm2$fitted.values, log2ESR1 = brca$log2ESR1)
brca %>%
  ggplot(aes(x= log2ESR1, y = log2S100A8)) +
  geom_point() +
  geom_point(aes(x=log2ESR1, y =lm2$fitted), pch = 2, size = 3, color = "red") +
  geom_smooth(method = "lm", se = FALSE,size=0.6, color = "red")  +
  geom_hline(aes(yintercept = mean(log2S100A8))) +
  geom_segment(data = lm2_df, aes(x = log2ESR1, xend = log2ESR1,
                                  y = fitted, yend =  mean(log2S100A8)), lty =2, color = "red") +
  ylab("S100A8 expressie (log2)") +
  xlab("ESR1 expressie (log2)")

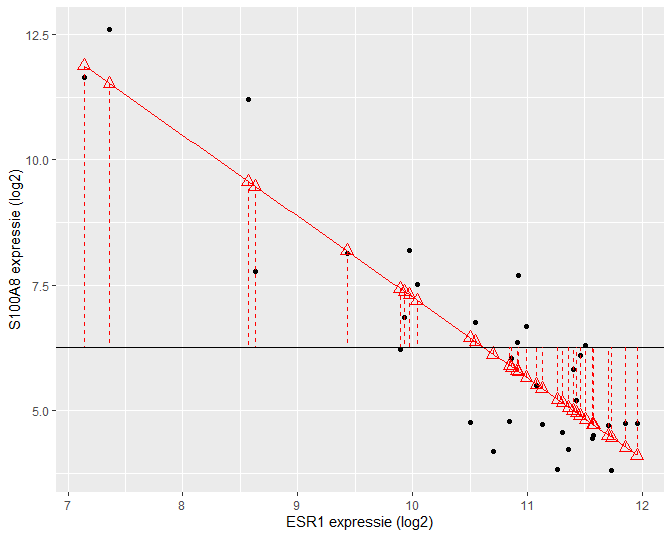
Figuur 37: Interpretatie van de kwadratensom van de regressie (SSR): de som van de kwadratische afwijkingen tussen de geschatte regressierechte en het steekproefgemiddelde van de uitkomsten.

Tenslotte herhalen we de kwadratensom van de fout:

\[\text{SSE} = \sum_{i=1}^n (Y_i-\hat{Y}_i )^2 = \sum_{i=1}^n \left\{Y_i-\hat{g}\left(x_i\right)\right\}^2.\]

Van SSE weten we reeds dat het een maat is voor de afwijking tussen de observaties en de predicties bij de geobserveerde \(x_i\) uit de steekproef. Hoe kleiner SSE, hoe beter de fit (schatting) van de regressierechte voor predictiedoeleinden. We hebben deze immers geminimaliseerd om tot de kleinste kwadratenschatters te komen.

Een interpretatie van SSE voor het log-log model wordt weergegeven in Figuur 38.

brca %>%
  ggplot(aes(x= log2ESR1, y = log2S100A8)) +
  geom_point() +
  geom_point(aes(x=log2ESR1, y =lm2$fitted), pch = 2, size = 3, color = "red") +
  geom_smooth(method = "lm", se = FALSE,size=0.6, color = "red")  +
  geom_segment(data = lm2_df, aes(x = log2ESR1, xend = log2ESR1,
                                  y = fitted, yend =  log2S100A8), lty =2, color = "black") +
  ylab("S100A8 expressie (log2)") +
  xlab("ESR1 expressie (log2)")

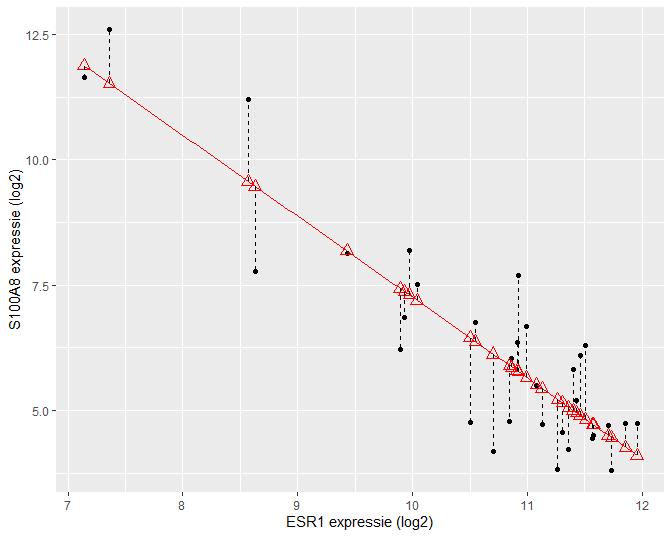
Figuur 38: Interpretatie van de kwadratensom van de error (SSE): de som van de kwadratische afwijkingen tussen uitkomsten en de predicties op de geschatte regressierechte.

Verder kan worden aangetoond dat de totale kwadratensom als volgt kan ontbonden worden

\[\begin{eqnarray*} \text{SSTot} &=& \sum_{i=1}^n (Y_i-\bar{Y})^2 \\ &=& \sum_{i=1}^n (Y_i-\hat{Y}_i+\hat{Y}_i-\bar{Y})^2 \\ &=& \sum_{i=1}^n (Y_i-\hat{Y}_i)^2+\sum_{i=1}^n(\hat{Y}_i-\bar{Y})^2 \\ &=& \text{SSE }+\text{SSR} \end{eqnarray*}\]

Merk op dat de dubbel product term wegvalt. Er kan aangetoond worden dat de ze gelijk is aan nul. Dat valt buiten het bestek van de ze cursus. De ontbinding van de totale kwadratensom kan als volgt worden geïnterpreteerd: De totale variabiliteit in de data (SSTot) wordt gedeeltelijk verklaard door het regressieverband (SSR). De variabiliteit die niet door het regressieverband verklaard wordt, is de residuele variabiliteit (SSE).