You may have heard of Pascal's triangle before. A triangular array that is constructed in the following way. At the top of the triangle you write the number 1. Each next row of the triangle is constructed by adding the two numbers above each cell in the row to find the new value in that cell. If either the number to the top right or top left is not present, substitute a zero in its place. Below we demonstrate how the first eleven rows of the triangle are constructed.
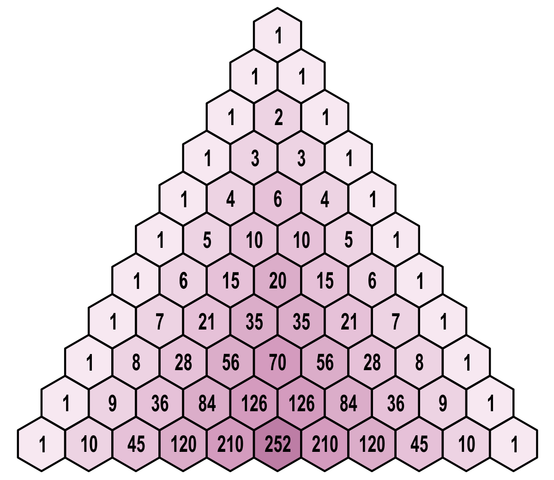
A remarkable feature of Pascal's triangle is that the product of the six numbers surrounding any interior position (a position not on the edge of the triangle) is a perfect square (a square of an integer number).
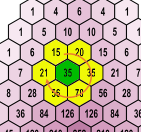
If we test this property for the number 35 on row 8 and column 4 in Pascal's triangle, we get \[15 \times 20 \times 35 \times 70 \times 56 \times 21 = 864360000 = 29400 \times 29400\]
Assignment
Test the above feature of Pascal's triangle. To reference the positions in Pascal's triangle we index the rows from top to bottom, and the columns on each row from left to right, each time starting at 1. You are asked to:
Write a function triangle that takes a number $$r \in \mathbb{N}$$. The function must return the first $$r$$ rows of Pascal's triangle, represented as a list of its rows from top to bottom. Each row is itself represented as a list of the numbers on that row from left to right. If the argument passed to the function is not a natural number, the function must raise an AssertionError with the message invalid number of rows.
Write a function hexagon that takes the row and column index of an internal position in Pascal's triangle. The function must return a list containing the six numbers surrounding that internal position, listed clockwise starting from the number to the top left of the given internal position.
Write a function square that takes the row and column index of an internal position in Pascal's triangle. The function must return a string that is formatted as factors = product = root x root, where factors is an expression representing the product of the six numbers surrounding the given internal position (listed in the same order as returned by the function hexagon, using x as the multiplication operator), product is the product of these six numbers, and root is the square root of this product expressed as an integer. Take a look at the examples below to see how the result needs to be formatted.
If the arguments passed to the functions hexagon and square do not represent an internal position in Pascal's triangle, both functions must raise an AssertionError with the message invalid internal position.
Example
>>> triangle(0)
[]
>>> triangle(1)
[[1]]
>>> triangle(2)
[[1], [1, 1]]
>>> triangle(3)
[[1], [1, 1], [1, 2, 1]]
>>> triangle(4)
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1]]
>>> triangle(5)
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]
>>> triangle(-1)
Traceback (most recent call last):
AssertionError: invalid number of rows
>>> triangle(3.14)
Traceback (most recent call last):
AssertionError: invalid number of rows
>>> hexagon(8, 4)
[15, 20, 35, 70, 56, 21]
>>> hexagon(16, 7)
[2002, 3003, 6435, 11440, 8008, 3003]
>>> hexagon(3, 3)
Traceback (most recent call last):
AssertionError: invalid internal position
>>> square(8, 4)
'15 x 20 x 35 x 70 x 56 x 21 = 864360000 = 29400 x 29400'
>>> square(16, 7)
'2002 x 3003 x 6435 x 11440 x 8008 x 3003 = 10643228293383247161600 = 103166022960 x 103166022960'
>>> square(3, 3)
Traceback (most recent call last):
AssertionError: invalid internal position