Een gerichte graaf bestaat uit een reeks knopen. Bij elke knoop $$A$$ hoort een verzameling doelknopen $$D_A$$. Een knoop $$B$$ behoort tot $$D_A$$ indien de graaf een gerichte tak bevat, vanuit $$A$$ naar $$B$$.

We stockeren de graaf in een woordenboek, waarbij elke knoop (een string) van de graaf als sleutel in dit woordenboek voorkomt. De bijhorende waarde is een verzameling van doelknopen (zoals hierboven gedefinieerd).

Schrijf een functie symmetrisch() met als enig argument een woordenboek dat een gerichte graaf voorstelt, zoals hierboven beschreven. Het resultaat van de functies is een verzameling van tuples. Elk van die tuples bestaat uit 2 strings, die elk een knoop van de graaf voorstellen. Het tuple $$(A, B)$$ komt in de resultaatverzameling voor als en slechts als de graaf een gerichte tak bevat van knoop $$A$$ naar knoop $$B$$ EN van knoop $$B$$ naar knoop $$A$$. Merk op dat, indien het tuple $$(A, B)$$ in de resultaatverzameling voorkomt, ook het tuple $$(B, A)$$ in het resultaat zal voorkomen.

Voorbeeld

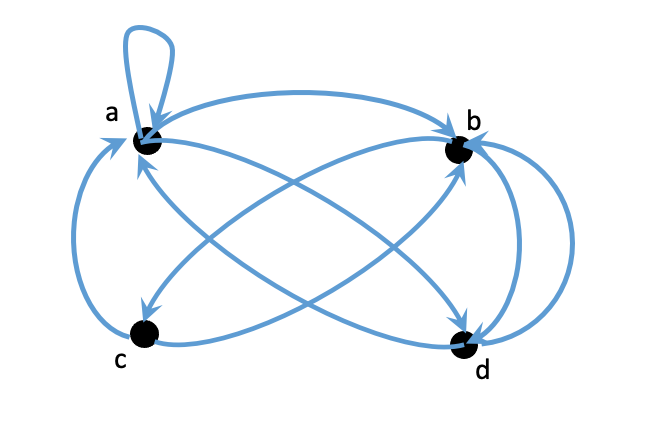
g = {'a':set(['a', 'b', 'd']), 'b':set(['c', 'd']), 'c':set(['b', 'a']), 'd':set(['a', 'b'])}
print(symmetrisch(g)) 
#{('d', 'b'), ('c', 'b'), ('a', 'a'), ('b', 'd'), ('b', 'c'), ('a', 'd'), ('d', 'a')}