All you need for this challenge is a deck of cards. Randomly draw some cards from the deck and line them up on a table in front of you, some cards face up, some cards face down. You can now remove any face up card, but you must also flip the adjacent cards (if any). The goal is to successfully remove every card. But beware: making the wrong move can get you stuck.

Let's demonstrate this with the following sequence of cards. To ease the explanation, we number the cards from left to right, starting from zero.

Leg een willekeurig aantal kaarten naast elkaar, waarbij sommige kaarten met hun beeldzijde naar boven liggen en de andere met hun beeldzijde naar onder.

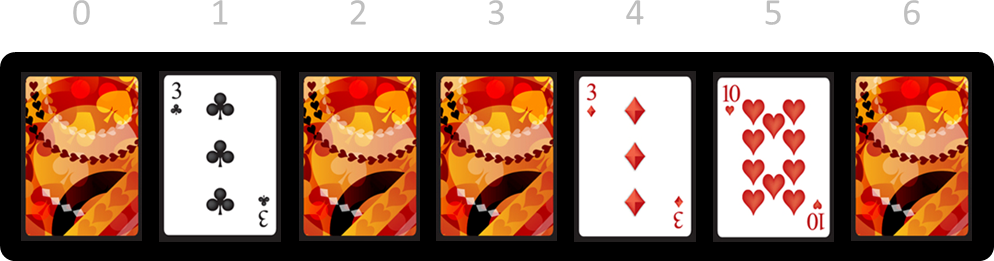
You can now choose to remove cards 1, 4 or 5 since these are face up. If you remove card 1, the sequence of cards looks like this (the red cross marks the position of the most recently removed card).

Verwijder kaart 1 en keer de twee aangrenzende kaarten 0 en 2 om.

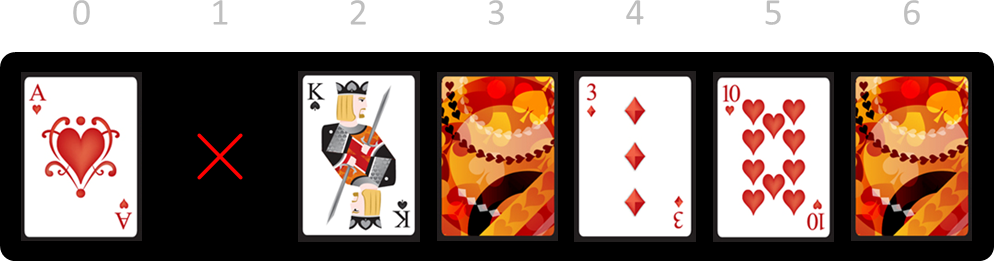
You had to flip cards 0 and 2 since they were adjacent. Next you could choose to remove cards 0, 2, 4 or 5. Let's say you decide to remove card 0.

Verwijder kaart 0. Omdat er naast die kaart geen andere kaarten liggen, moet je dus ook geen kaarten omkeren.

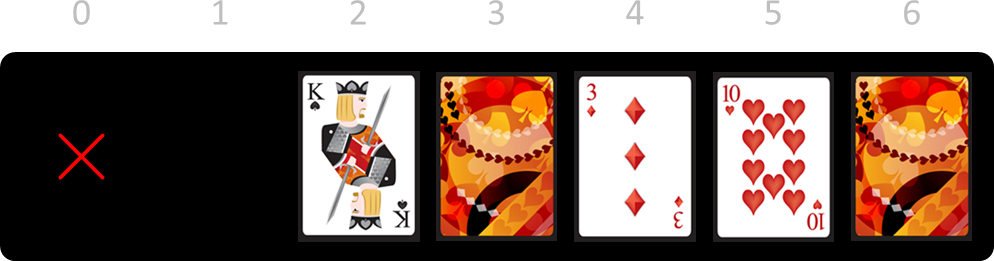
Since card 0 has no adjacent cards, there were no cards to flip. You can win this game by continuing with the removal of cards 2, 3, 5, 4 and 6.

Je kan het spel winnen door nu achtereenvolgens kaarten 2, 3, 5, 4 en 6 te verwijderen.

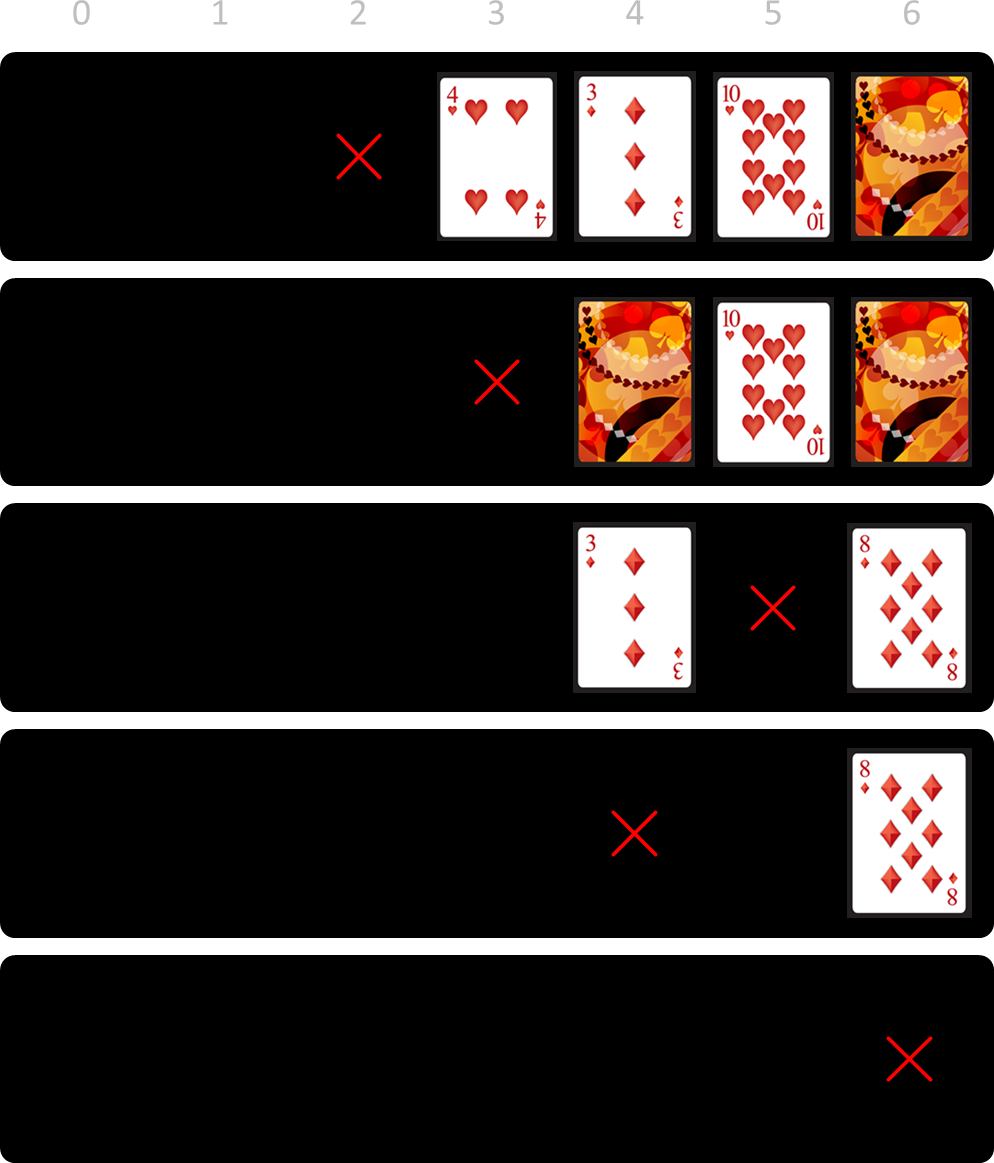
This won't always work. Suppose you had started removing card 4.

Verwijder kaart 4 en keer de twee aangrenzende kaarten 3 en 5 om.

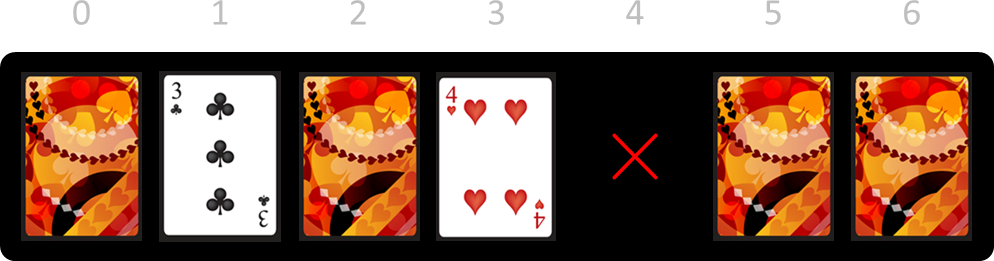
This is unsolvable since there's an "island" of cards at the right, with all cards face down. Cards in such an island can never be flipped face up, so that they can't be remove neither.

Assignment

A standard card deck includes 52 different cards, evenly distributed over four suits: 13 clubs (♣), 13 diamonds (♦), 13 hearts (♥) and 13 spades (♠). Clubs and spades are black, whereas diamonds and hearts are red. Each suit includes thirteen ranks: two through ten (with each card depicting that many symbols of its suit), jack, queen, king (each depicted with a symbol of its suit) and ace (depicting a single symbol of its suit). Commercial card decks may also include anywhere from one to six jokers, but we do not take these into account here.

Each card of a standard 52-card deck is represented by a string that contains the rank of the card, followed by its suit:

ranks: 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), K (king) and A (ace)
suits: C (clubs; ♣), D (diamonds; ♦), H (hearts; ♥) and S (spades; ♠)

As such, the ace of spades is for example represented as AS, the ten of hearts as 10H and the king of clubs as KC. In addition we use uppercase for face-up cards (e.g. AS or 10H) and lowercase for face-down cards (e.g. as or 10h). Note that the last character of the string representation of a card is always an uppercase or lowercase letter (not a digit) that indicates the suit of the card.

Define a class Cards that can be used to represent a sequence of cards, with some cards facing up and others facing down. A sequence of cards does not necessarily have to contain all 52 cards of a deck, but each card may occur at most once. When creating an object of the class Cards, a sequence (list or tuple) with the string representations of the cards must be passed. If no valid sequence of cards is passed, an AssertionError must be raised with the message invalid cards.

Make sure the conversion of an object $$o$$ of class Cards into a string (str) — obtained using the built-in function str — yields a sequence of cards as represented in the interactive session below. This consists of the representations of the successive cards in the sequence, using a single space as a separator. A card that is facing up is represented in the standard way. A card that faces down is represented by two asterisks (**). A removed card is represented by a greater then sign, followed by a less than sign (><).

In addition, the class Cards must support at least the following methods:

A method remove that either takes the number (int) or the string representation (str) of a face up card from the sequence. If the argument does not indicate a card facing up, an AssertionError must be raised with the message invalid card. Otherwise, the card must be removed, and the two adjacent cards must be flipped (if any). The method must return a reference to the object on which the method was called.
A method islands that takes no arguments. The method must return the number of islands that are formed by the cards that have no yet been removed. An island is the longest possible sequence of neighboring cards, with no intermediate positions where cards have been removed.
A method haswon that takes no arguments. The method must return a Boolean value (bool) that indicates whether the game has been won. This is the case if all cards have been removed.

Example

        >>> cards = Cards(['ah', '3S', 'kc', '4h', '3D', '10H', '8d'])
>>> print(cards)
** 3S ** ** 3D 10H **
>>> cards.islands()
1
>>> cards.haswon()
False
>>> print(cards.remove(1))
AH >< KC ** 3D 10H **
>>> cards.remove(1)
Traceback (most recent call last):
AssertionError: invalid card
>>> cards.remove(3)
Traceback (most recent call last):
AssertionError: invalid card
>>> cards.remove(-3)
Traceback (most recent call last):
AssertionError: invalid card
>>> cards.remove(42)
Traceback (most recent call last):
AssertionError: invalid card
>>> print(cards.remove('AH'))
>< >< KC ** 3D 10H **
>>> cards.islands()
1
>>> cards.haswon()
False
>>> print(cards.remove('AH'))
Traceback (most recent call last):
AssertionError: invalid card
>>> print(cards.remove('QS'))
Traceback (most recent call last):
AssertionError: invalid card
>>> print(cards.remove(2).remove(3))
>< >< >< >< ** 10H **
>>> cards.islands()
1
>>> cards.haswon()
False
>>> print(cards.remove('10h').remove('3d').remove('8d'))
>< >< >< >< >< >< ><
>>> cards.islands()
0
>>> cards.haswon()
True

>>> Cards(['ah', '3S', 'kc', '4h', '3D', 'AH', '8d'])
Traceback (most recent call last):
AssertionError: invalid cards
>>> Cards(['ah', '3S', 'kc', '4h', '3D', 42, '8d'])
Traceback (most recent call last):
AssertionError: invalid cards
>>> Cards(['ah', '3S', 'kc', '4h', '3D', 'XD', '8d'])
Traceback (most recent call last):
AssertionError: invalid cards
>>> Cards(['ah', '3S', 'kc', '4h', '3D', 'AY', '8d'])
Traceback (most recent call last):
AssertionError: invalid cards
>>> Cards({'ah', '3S', 'kc', '4h', '3D', '10H', '8d'})
Traceback (most recent call last):
AssertionError: invalid cards