A Spelling Bee is a word puzzle with a given collection of different letters. One of those letters is marked as "mandatory". The goal is to find as many existing words as possible that can be spelled with the given letters. Words do not need to use all letters in the puzzle, may use the same letter more than once, but must contain at least the mandatory letter.

Puzzles differ not only in which letters are given, but also in the number of letters given, the minimum number of letters the words must have to qualify as a solution and the dictionary used to determine which words actually exist. Here are three sample puzzles with 7, 9 and 13 given letters respectively, and their mandatory letter indicated by the yellow cell.

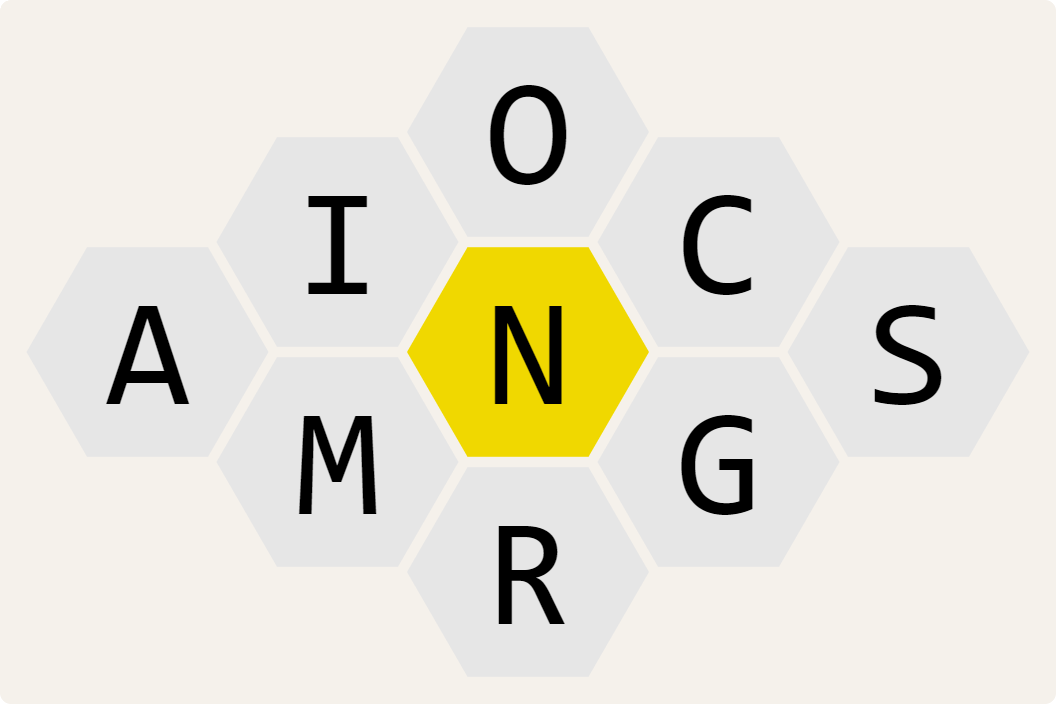
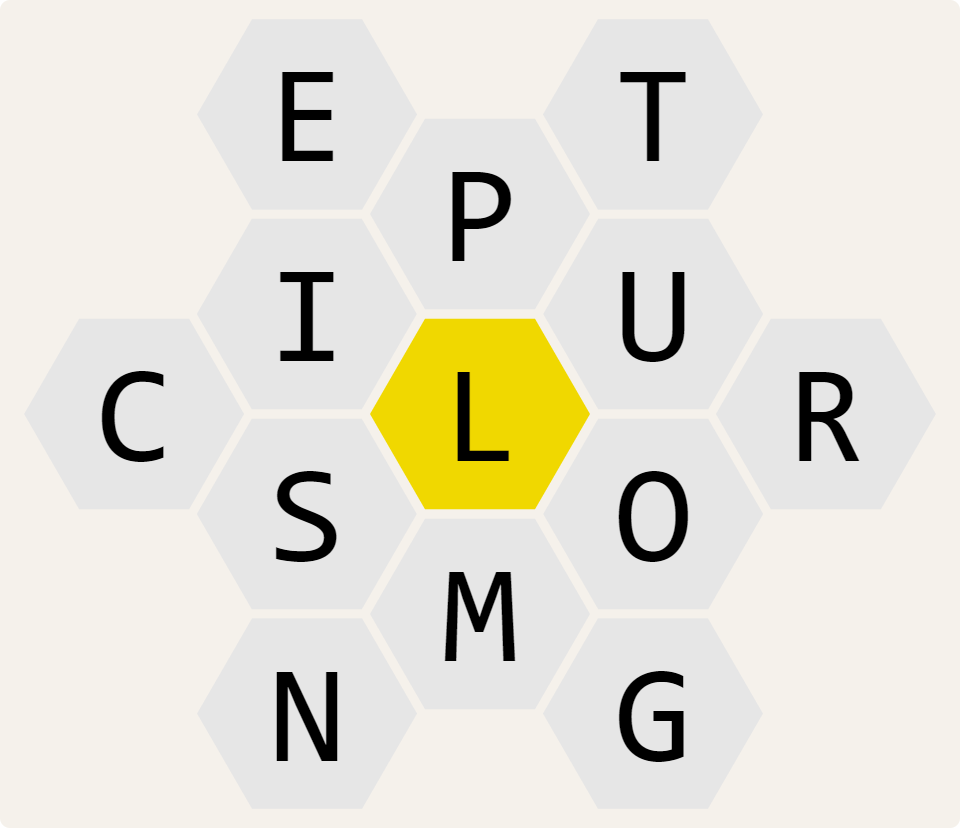
Usually, each puzzle has at least one hidden pangram: a word that contains all letters of the puzzle at least once. This is the case for the above puzzles: hopelessness is a pangram for the left puzzle, multiprocessing is a pangram for the right puzzle and the middle puzzle even has two pangrams with microorganism and microorganisms.

Assignment

Write functions that can determine all solutions or all pangrams of a given puzzle. These functions may assume that all words and puzzles passed to them are strings (str) consisting only of letters (both uppercase and lowercase), without having to check this explicitly. Each uppercase letter in a puzzle represents a mandatory letter and each lowercase letter represents an optional letter (which is not mandatory). Your task:

• Write a function isspellable that takes two words $$w_1$$ and $$w_2$$ (str). The function may assume that all letters of word $$w_2$$ are different, without having to check this explicitly. The function must return a Boolean value (bool) that indicates whether word $$w_1$$ can be spelled with the letters of word $$w_2$$. This is the case if all the letters of word $$w_1$$ also appear in word $$w_2$$, without distinguishing between uppercase and lowercase letters.

• Write a function ispangram that takes two words $$w_1$$ and $$w_2$$ (str). The function may assume that all letters of word $$w_2$$ are different, without having to check this explicitly. The function must return a Boolean value (bool) that indicates whether word $$w_1$$ is a pangram of word $$w_2$$. This is the case if word $$w_1$$ can be spelled with the letters of word $$w_2$$ and contains all the letters of word $$w_2$$ at least once, without distinguishing between uppercase and lowercase letters.

• Write a function solutions that takes two arguments: i) the location (str) of a text file containing a sequence of words, each on a separate line and ii) a puzzle $$p$$ (str). The function also has a third optional parameter minimum that may take a positive natural number $$m$$ (int; default value: 4). If puzzle $$p$$ contains duplicate letters (without distinguishing between uppercase and lowercase letters) or if puzzle $$p$$ does not consist of lowercase letters and one uppercase letter, an AssertionError must be raised with the message invalid puzzle. Otherwise, the function must return a set containing all words from the given text file that are solutions of puzzle $$p$$: words that i) can be spelled with the letters of puzzle $$p$$, ii) contain the mandatory letter of puzzle $$p$$ and iii) are at least $$m$$ letters long.

• Write a function pangrams that takes two arguments: i) the location (str) of a text file containing a sequence of words, each on a separate line and ii) a puzzle $$p$$ (str). If puzzle $$p$$ contains duplicate letters (without distinguishing between uppercase and lowercase letters) or if puzzle $$p$$ does not consist of lowercase letters and one uppercase letter, an AssertionError must be raised with the message invalid puzzle. Otherwise, the function must return a set containing all words from the given text file that aside from being solutions are also pangrams of puzzle $$p$$.

Example

In the following interactive session, we assume the text file words.txt¹ is located in the current directory.

>>> isspellable('houseplant', 'oesHpln')
False
>>> isspellable('phone', 'oesHpln')
True
>>> isspellable('epsilon', 'oesHpln')
False
>>> isspellable('loophole', 'oesHpln')
True

>>> ispangram('helplessness', 'oesHpln')
False
>>> ispangram('hopelessness', 'oesHpln')
True

>>> solutions('words.txt2', 'oesHpln')
{'hones', 'hellos', 'hopelessness', 'shone', 'hopes', 'shoon', 'hellholes', 'heels', 'nosh', 'shoos', 'hello', 'hoop', 'hell', 'loopholes', 'shells', 'hoes', 'loophole', 'noshes', 'hopeless', 'phones', 'sloshes', 'hens', 'shes', 'helplessness', 'holes', 'shell', 'hops', 'peepholes', 'hose', 'pooh', 'hope', 'posh', 'phone', 'hellhole', 'shleps', 'shlepps', 'shoe', 'shlep', 'shops', 'poohs', 'shop', 'shoes', 'slosh', 'sheep', 'hole', 'helpless', 'hoops', 'helps', 'hoses', 'help', 'shlepp', 'shoo', 'hone', 'peephole', 'sheen', 'heel'}
>>> solutions('words.txt3', 'oesHpln', minimum=10)
{'hopelessness', 'helplessness'}
>>> solutions('words.txt4', 'ocgrNminas')     # two occurrences of letter N
Traceback (most recent call last):
AssertionError: invalid puzzle
>>> solutions('words.txt5', 'LpuomsietrgnC')  # two capitals
Traceback (most recent call last):
AssertionError: invalid puzzle

>>> pangrams('words.txt6', 'oesHpln')
{'hopelessness'}
>>> pangrams('words.txt7', 'ocgrNmias')
{'microorganism', 'microorganisms'}
>>> pangrams('words.txt8', 'Lpuomsietrgnc')
{'multiprocessing'}

Epilogue

A spelling bee is a competition in which contestants are asked to spell a broad selection of words, usually with a varying degree of difficulty. Contestants must memorize the spellings of the words as written in dictionaries, and recite them accordingly.

Spelling bees became widespread across the United States during the 1800s, as a way to motivate students to learn standardized spelling. The Scripps National Spelling Bee⁹ — the annual United States national spelling bee — was started in 1925 and has now become so famous that the winner (and the word they won with) can count on making national headlines and network news shows. Have the words gotten tougher over the years? Judge for youself:

• the 1920s: gladiolus (1925), abrogate (1926), luxuriance (1927), albumen (1928), asceticism (1929)

• the 1930s: fracas (1930), foulard (1931), knack (1932), torsion (1933), deteriorating (1934), intelligible (1935), interning (1936), promiscuous (1937), sanitarium (1938), canonical (1939)

• the 1940s: therapy (1940), initials (1941), sacrilegious (1942), semaphore (1946), chlorophyll (1947), psychiatry (1948), dulcimer (1949)

• the 1950s: meerschaum / meticulosity (1950), insouciant (1951), vignette (1952), soubrette (1953), transept (1954), crustaceology (1955), condominium (1956), schappe (1957), syllepsis (1958), catamaran (1959)

• the 1960s: eudaemonic (1960), smaragdine (1961), esquamulose (1962), equipage (1963), sycophant (1964), eczema (1965), ratoon (1966), chihuahua (1967), abalone (1968), interlocutory (1969)

• the 1970s: croissant (1970), shalloon (1971), macerate (1972), vouchsafe (1973), hydrophyte (1974), incisor (1975), narcolepsy (1976), cambist (1977), deification (1978), maculature (1979)

• the 1980s: elucubrate (1980), sarcophagus (1981), psoriasis (1982), Purim (1983), luge (1984), milieu (1985), odontalgia (1986), staphylococci (1987), elegiacal (1988), spoliator (1989)

• the 1990s: fibranne (1990), antipyretic (1991), lyceum (1992), kamikaze (1993), antediluvian (1994), xanthosis (1995), vivisepulture (1996), euonym (1997), chiaroscurist (1998), logorrhea (1999)

• the 2000s: demarche (2000), succedaneum (2001), prospicience (2002), pococurante (2003), autochthonous (2004), appoggiatura (2005), Ursprache (2006), serrefine (2007), guerdon (2008), Laodicean (2009)

• the 2010s: stromuhr (2010), cymotrichous (2011), guetapens (2012), knaidel (2013), stichomythia / feuilleton (2014), scherenschnitte / nunatak (2015), Feldenkrais / gesellschaft (2016), marocain (2017), koinonia (2018), auslaut / erysipelas / bougainvillea / aiguillette / pendeloque / palama / cernuous / odylic (2019)

• the 2020s: Murraya (2021), moorhen (2022), psammophile (2023), abseil (2024)