Ergens midden 2030 genieten 50000 toeschouwers van een wedstrijd robotvoetbal in het nieuwe Heizelstadion te Brussel. In de 63e minuut opent een terrorist een proefbuisje met een uiterst dodelijk virus. Het virus verspreidt zich zo snel dat elke minuut de helft van het nog overblijvend aantal toeschouwers sterft.

De functie $$f$$ die het resterend aantal toeschouwers na een zekere tijd beschrijft, heeft volgend voorschrift:

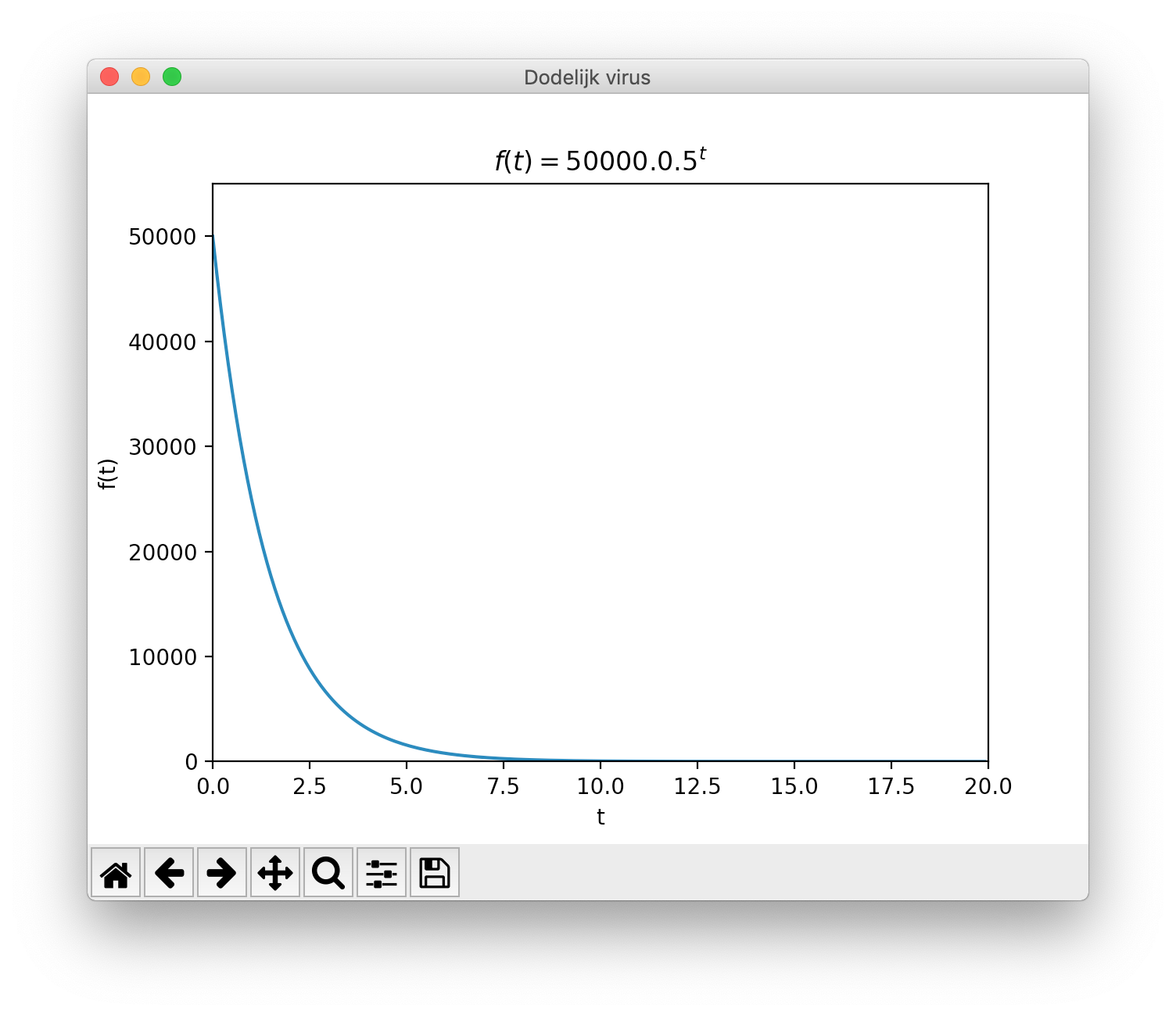
\[f: t \mapsto 50000 . 0,5^{t}\]

Hierbij stelt $$t \in \mathbb{R}^{+}$$ het aantal minuten voor sinds het openen van de proefbuis.

Opgave

Vraag aan de gebruiker van het programma het aantal minuten $$t \in \mathbb{R}^{+}$$ na het openen van de proefbuis. Geef het nog overblijvend aantal toeschouwers op, afgerond tot op een eenheid.

Wat is NIET toegelaten:

• De format-functie;
• De machtsverheffing met de **-operator.

Voorbeeld

0

50000

Voorbeeld

3.343

4927