Given an amino acid string $$p$$, we will begin by assuming that it represents a linear peptide. Our approach to generating its theoretical spectrum is based on the assumption that the mass of any subpeptide is equal to the difference between the masses of two prefixes of $$p$$. We can compute an array PrefixMass storing the masses of each prefix of $$p$$ in increasing order, e.g., for $$p$$ = NQEL

PrefixMass = (0, 114, 242, 371, 484)

Then, the mass of the subpeptide of $$p$$ beginning at position $$i + 1$$ and ending at position $$j$$ can be computed as

PrefixMass($$j$$) - PrefixMass($$i$$)

For example, when $$p$$ = NQEL,

Mass(QE) = PrefixMass(3) - PrefixMass(1) = 371 - 114 = 257

The pseudocode shown below implements this idea.

LinearSpectrum(Peptide, AminoAcid, AminoAcidMass)
    PrefixMass(0) ← 0
    for i ← 1 to |Peptide|
        for j ← 1 to 20
            if AminoAcid(j) = i-th amino acid in Peptide
                PrefixMass(i) ← PrefixMass(i − 1) + AminoAcidMass(j)
    LinearSpectrum ← a list consisting of the single integer 0
    for i ← 0 to |Peptide| − 1
        for j ← i + 1 to |Peptide|
            add PrefixMass(j) − PrefixMass(i) to LinearSpectrum
    return sorted list LinearSpectrum

It also represents the alphabet of 20 amino acids and their integer masses as a pair of 20-element arrays AminoAcid and AminoAcidMass, corresponding to the top and bottom rows of the following integer mass table, respectively.

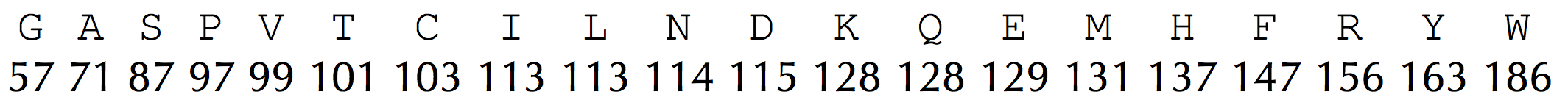
Assignment

In this and all following assignments, we represent a peptide $$p$$ (a short amino acid string) as a tuple containing the (possibly repeated) integer masses of the individual amino acids in the peptide. In case of a cyclic peptide, its tuple representation is cyclic as well, and we choose the representation that comes first in lexicographic order. A spectrum is represented as a tuple of (possibly repeated) integers, sorted in increasing order. Your task:

• Write a function linear_spectrum that takes a peptide $$p$$. The function must return the theoretical spectrum of the linear peptide.

Example

>>> linear_spectrum('NQEL')
(0, 113, 114, 128, 129, 242, 242, 257, 370, 371, 484)