Regressiediagnostieken
Multicollineariteit
Het is interessant om in de R output voor het model met lcavol:lweight interactie ook naar schattingen van de hoofdeffecten te kijken (Sectie 10.5.2). De waarden van de schattingen zijn niet alleen verschillend van wat we in het additieve model vonden, maar de standaardfouten zijn nu veel groter! De oorzaak moet gezocht worden in het probleem van multicollineariteit. Wanneer 2 predictoren sterk gecorreleerd zijn, dan delen ze voor een groot stuk dezelfde informatie en is het moeilijk om de afzonderlijke effecten van beiden op de uitkomst te schatten. Dit uit zich in het feit dat de computationele berekening van de kleinste kwadratenschatters onstabiel wordt, in die zin dat kleine wijzigingen aan de gegevens of het toevoegen of weglaten van een predictorvariabele een belangrijke impact kunnen hebben op de grootte, en zelfs het teken, van de geschatte regressieparameters. Een tweede effect van multicollineariteit is dat standaard errors bij de geschatte regressieparameters fel kunnen worden opgeblazen en de bijhorende betrouwbaarheidsintervallen bijgevolg zeer breed kunnen worden. Zolang men enkel predicties tracht te bekomen op basis van het regressiemodel zonder daarbij te extrapoleren buiten het bereik van de predictoren is multicollineariteit geen probleem.
cor(cbind(prostate$lcavol,prostate$lweight,prostate$lcavol*prostate$lweight))
## [,1] [,2] [,3]
## [1,] 1.0000000 0.1941283 0.9893127
## [2,] 0.1941283 1.0000000 0.2835608
## [3,] 0.9893127 0.2835608 1.0000000
We zien dat de correlatie inderdaad erg hoog is tussen het log-tumorvolume en de interactieterm. Het is gekend dat hogere orde termen (interacties en kwadratische termen) vaak een sterke correlatie vertonen.
Problemen als gevolg van multicollineariteit kunnen herkend worden aan het feit dat de resultaten onstabiel worden. Zo kunnen grote wijzigingen optreden in de parameters na toevoeging van een predictor, kunnen zeer brede betrouwbaarheidsintervallen bekomen worden voor sommige parameters of kunnen gewoonweg onverwachte resultaten worden gevonden. Meer formeel kan men zich een idee vormen van de mate waarin er van multicollineariteit sprake is door de correlaties te inspecteren tussen elk paar predictoren in het regressiemodel of via een scatterplot matrix die elk paar predictoren uitzet op een scatterplot. Dergelijke diagnostieken voor multicollineariteit zijn echter niet ideaal. Vooreerst geven ze geen idee in welke mate de geobserveerde multicollineariteit de resultaten onstabiel maakt. Ten tweede kan het in modellen met 3 of meerdere predictoren, zeg X1, X2, X3, voorkomen dat er zware multicollineariteit is ondanks het feit dat alle paarsgewijze correlaties tussen de predictoren laag zijn. Dit kan bijvoorbeeld optreden wanneer de correlatie hoog is tussen X1 en een lineaire combinatie van X2 en X3.
Bovenstaande nadelen kunnen vermeden worden door de te onderzoeken, die voor de \(j\)-de parameter in het regressiemodel gedefinieerd wordt als
\[\textrm{VIF}_j=\left(1-R_j^2\right)^{-1}\]In deze uitdrukking stelt \(R_j^2\) de meervoudige determinatiecoëfficiënt voor van een lineaire regressie van de \(j\)-de predictor op alle andere predictoren in het model. De VIF heeft de eigenschap dat ze gelijk is aan 1 indien de \(j\)-de predictor niet lineair geassocieerd is met de andere predictoren in het model, en bijgevolg wanneer de \(j\)-de parameter in het model niet onderhevig is aan het probleem van multicollineariteit. De VIF is groter dan 1 in alle andere gevallen. In het bijzonder drukt ze uit met welke factor de geobserveerde variantie op de schatting voor de \(j\)-de parameter groter is dan wanneer alle predictoren onafhankelijk zouden zijn. Hoe groter de VIF, hoe minder stabiel de schattingen bijgevolg zijn. Hoe kleiner de VIF, hoe dichter de schattingen dus bij de gezochte populatiewaarden verwacht worden. In de praktijk spreekt men van ernstige multicollineariteit voor een regressieparameter wanneer haar VIF de waarde 10 overschrijdt.
We illustreren dat a.d.h.v. onderstaande voorbeeld.
Voorbeeld vetpercentage
Het percentage lichaamsvet van een persoon bepalen is een moeilijke en dure meting. Om die reden werden in het verleden verschillende studies opgezet met als doel het patroon te ontrafelen tussen werkelijk percentage lichaamsvet en verschillende, makkelijker te meten surrogaten. In een studie heeft men voor 20 gezonde vrouwen tussen 25 en 34 jaar het percentage lichaamsvet \(Y\), de dikte van de huidplooi rond de triceps \(X_1\), de dij-omtrek \(X_2\) en de middenarmomtrek \(X_3\) gemeten. Indien we een nauwkeurig regressiemodel kunnen opstellen op basis van de gegevens, dan zal ons dat toelaten om in de toekomst met behulp van dat model voorspellingen te maken voor het percentage lichaamsvet in gezonde vrouwen tussen 25 en 34 jaar, op basis van de huidplooi rond de triceps, de dij-omtrek en de middenarmomtrek.
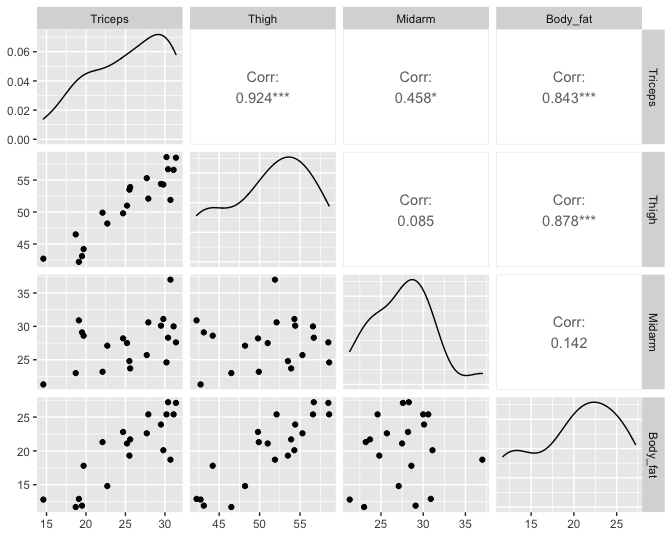
Figuur 65: Scatterplot matrix van de dataset bodyfat.
Wanneer we de 3 predictoren simultaan aan een regressiemodel toevoegen, bekomen we de volgende output.
lmFat <- lm(Body_fat ~ Triceps + Thigh + Midarm, data = bodyfat)
summary(lmFat)
##
## Call:
## lm(formula = Body_fat ~ Triceps + Thigh + Midarm, data = bodyfat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7263 -1.6111 0.3923 1.4656 4.1277
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.085 99.782 1.173 0.258
## Triceps 4.334 3.016 1.437 0.170
## Thigh -2.857 2.582 -1.106 0.285
## Midarm -2.186 1.595 -1.370 0.190
##
## Residual standard error: 2.48 on 16 degrees of freedom
## Multiple R-squared: 0.8014, Adjusted R-squared: 0.7641
## F-statistic: 21.52 on 3 and 16 DF, p-value: 7.343e-06
vif(lmFat)
## Triceps Thigh Midarm
## 708.8429 564.3434 104.6060
Hoewel het model meer dan 80% van de variabiliteit in het vetpercentage kan verklaren en dat de F-test die test voor alle predictoren simultaan extreem significant is, is de associatie echter voor geen enkele predictor significant volgens de individuele t-testen. De scatterplot matrix in Figuur 65 geeft aan dat er multicollineariteit aanwezig is wat betreft de predictoren \(X_1\) en \(X_2\), maar niet meteen wat betreft de middenarmomtrek \(X_3\). Niettemin bekomen we erg hoge VIFs voor alle model parameters. Dit suggereert dat ook de middenarmomtrek gevoelig is aan ernstige multicollineariteit en bijgevolg dat scatterplot matrices inderdaad slechts een beperkt licht werpen op het probleem van multicollineariteit. De VIF varieert van 105-709, hetgeen aantoont dat de (kwadratische) afstand tussen de schattingen voor de regressieparameters en hun werkelijke waarden 105 tot 709 keer hoger kan worden verwacht dan wanneer er geen multicollineariteit zou zijn. Hoewel de paarsgewijze correlatie tussen Midarm en Triceps en Midarm en Thigh laag is, toont de regressie van Midarm op Triceps en Thigh echter aan dat beide variabelen samen 99% van de variabiliteit in de variabiliteit van Midarm kunnen verklaren, wat er voor zorgt dat er ook voor Midarm een extreem hoge multicollineariteit is.
lmMidarm <- lm(Midarm ~ Triceps + Thigh, data = bodyfat)
summary(lmMidarm)
##
## Call:
## lm(formula = Midarm ~ Triceps + Thigh, data = bodyfat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.58200 -0.30625 0.02592 0.29526 0.56102
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 62.33083 1.23934 50.29 <2e-16 ***
## Triceps 1.88089 0.04498 41.82 <2e-16 ***
## Thigh -1.60850 0.04316 -37.26 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.377 on 17 degrees of freedom
## Multiple R-squared: 0.9904, Adjusted R-squared: 0.9893
## F-statistic: 880.7 on 2 and 17 DF, p-value: < 2.2e-16
Einde voorbeeld
We evalueren nu de VIF in het prostaatkanker voorbeeld voor het additieve model en het model met interactie.
vif(lmVWS)
## lcavol lweight svi
## 1.447048 1.039188 1.409189
vif(lmVWS_IntVW)
## lcavol lweight svi lcavol:lweight
## 76.193815 1.767121 1.426646 80.611657
We zien dat de variance inflation factors voor het additieve model laag zijn, ze liggen allen dicht bij 1. Deze voor het model met interactie zijn echter hoog, voor lcavol en de interactie liggen ze respectievelijk op 76.2 en 80.6. Wat wijst op zeer ernstige multicollineariteit.
Merk op dat dit voor interactietermen vaak wordt veroorzaakt door het feit dat het hoofdeffect een andere interpretatie krijgt. Voor lcavol wordt dit b.v. het effect van het log-tumorvolume bij een log-prostaatgewicht van 0. Dit kan uiteraard niet voorkomen, alle log-prostaatgewichten liggen tussen 2.37 en 6.108 en berust dus op sterke extrapolatie. In de literatuur wordt daarom vaak voorgesteld om de variabelen te centreren rond het gemiddelde wanneer men hogere orde termen in het model opneemt. Dat is echter niet nodig, we weten immers dat het effect van het log-tumorvolume in het model met de lcavol:lweight interactie niet kan worden bestudeerd zonder het log-prostaatgewicht in rekening te brengen. We zullen in de practica zien dat we i.p.v. de data te centreren evengoed een test kunnen uitvoeren voor het effect van lcavol bij het gemiddelde log-prostaatgewicht, wat de interpretatie is voor het effect van lcavol bij het gecentreerde model.