Aachen University physicist Jörg Pretz has devised a binary clock in the shape of a triangular array of 15 lamps.
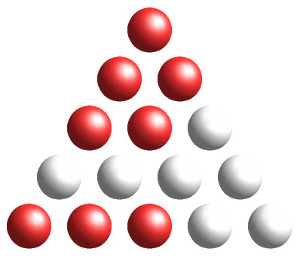
Here's how to read it:
- when lit, the top lamp denotes 6 hours
- each lamp on the second row denotes 2 hours
- each lamp on the third row denotes 30 minutes
- each lamp on the fourth row denotes 6 minutes
- each lamp on the bottom row denotes 1 minute
So the clock above shows the following time: \[ 6\ \textrm{hours} + (2 \times 2\ \textrm{hours}) + (2 \times 30\ \textrm{minutes}) + (3 \times 1\ \textrm{minute}) = 11\!:\!03 \] The fact that the lamps have a red color shows that it's afternoon, or 23:03 on a 24-hour clock. The same array of lamps would be displayed in green at 11:03 in the morning. Here are some more examples:


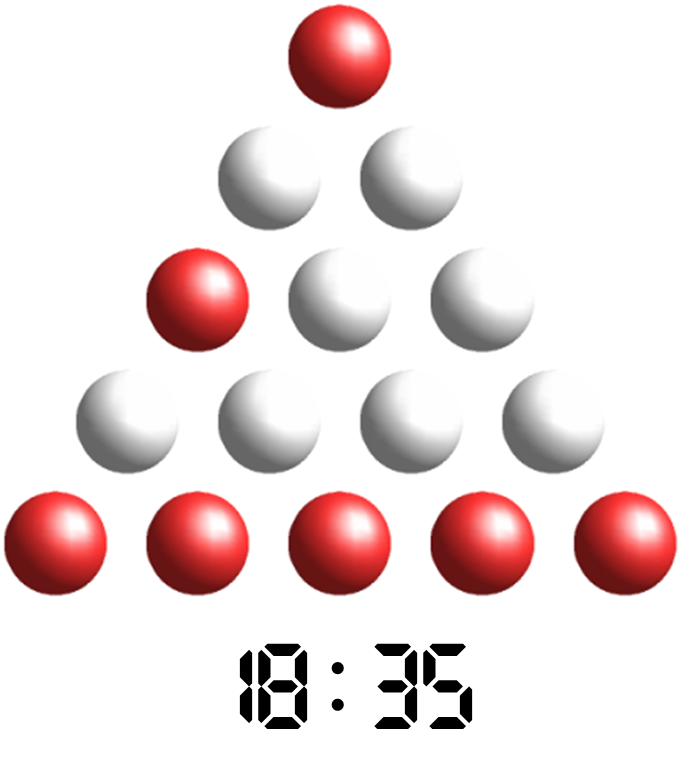

The time value assigned to each lamp is the total time value of the row below if that row contained one additional lamp. On each row the lamps light up from left to right, so a row with $$n$$ lamps can display $$n + 1$$ states (all lamps off to all lamps on). So for a triangular array with $$n$$ lamps on the bottom row, the total number of states is \[ (n + 1) \times ((n - 1) + 1) \times ((n - 2) + 1) \times \cdots \times (1 + 1) = (n + 1)! \] That is, it's a factorial of a natural number. And by a happy coincidence, the total number of minutes in 12 hours is such a factorial ($$12 \times 60 = 720 = 6!$$). Jörg Pretz's article mentions the following:
Thus the whole concept works because our system of time divisions is based on a sexagesimal system dating back to the Babylonians, rather than a decimal system as proposed during the French Revolution.
However, the clock has a small design error: with all lamps turned off it doesn't tell whether it's midnight (00:00) or noon (12:00). Technically speaking we consider 00:00 to be the first minute of the morning (zero green lamps lit on each row) and 12:00 to be the first minute of the afternoon (zero red lamps lit on each row).
Assignment
Define a class Clock that implements triangular clocks in Python. This class must support at least the following methods:
-
An initialization method that takes two natural numbers, indicating the hours $$h$$ ($$0 \leq h < 24$$) and minutes $$m$$ ($$0 \leq m < 60$$) on a 24-hour clock. If the arguments are not integers within the given intervals, an AssertionError must be raised with the message invalid time.
-
A method updateHours with an optional parameter that may take a number $$h \in \mathbb{Z}$$ (default value: 1). The method must move the current time of the clock forward (if $$h > 0$$) or backward (if $$h < 0$$) with the given number of hours $$h$$. In doing so, it must take into account that 23 hours is followed by 0 hours on a 24-hour clock, and likewise that 0 hours is preceded by 23 hours. The method must return a reference to the object on which the method was called.
-
A method updateMinutes with an optional parameter that may take a number $$m \in \mathbb{Z}$$ (default value: 1). The method must move the current time of the clock forward (if $$m > 0$$) or backward (if $$m < 0$$) with the given number of minutes $$m$$. In doing so, it must take into account that 23:59 is followed by 00:00 on a 24-hour clock, and likewise that 00:00 is preceded by 23:59. The method must return a reference to the object on which the method was called.
-
A method lamps that takes no arguments. The method must return a tuple containing two elements: i) a tuple containing five natural numbers that indicate the number of lamps that are lit on each row of the triangular clock (listed from the top to the bottom row) and ii) a single character that indicates the color of the lamps: G for green or R for red.
-
A method __repr__ that returns a string representation of the object. This string must contain a Python statement that indicates how to instantiate an object of the class Clock that is set to the current time of the object on which the method was called. Take a look at the example below to see how the string representation must be formatted.
-
A method __str__ that returns a string representation of the object. This string must contain a graphical representation of the triangular clock, in which each row of the clock is displayed on a separate line. The lamps on each row are represented by a single character: G for a lamp that is lit in the morning, R for a lamp that is lit in the afternoon and a dot (.) for a lamp that is turned off. The characters for the lamps on the same row are separated from each other by a single space, and leading spaces are prepended to each line (except for the last line) to obtain a triangular representation. None of the lines ends with spaces. Take a look at the example below to see how the string representation must be formatted.
Example
>>> clock = Clock(11, 3)
>>> clock.lamps()
((1, 2, 2, 0, 3), 'G')
>>> clock
Clock(11, 3)
>>> print(clock)
G
G G
G G .
. . . .
G G G . .
>>> clock.updateHours()
Clock(12, 3)
>>> clock.lamps()
((0, 0, 0, 0, 3), 'R')
>>> clock.updateHours(11)
Clock(23, 3)
>>> clock.lamps()
((1, 2, 2, 0, 3), 'R')
>>> print(clock)
R
R R
R R .
. . . .
R R R . .
>>> clock.updateMinutes()
Clock(23, 4)
>>> clock.lamps()
((1, 2, 2, 0, 4), 'R')
>>> clock.updateMinutes(42)
Clock(23, 46)
>>> clock.lamps()
((1, 2, 3, 2, 4), 'R')
>>> print(clock)
R
R R
R R R
R R . .
R R R R .
>>> clock.updateMinutes(13)
Clock(23, 59)
>>> clock.lamps()
((1, 2, 3, 4, 5), 'R')
>>> print(clock)
R
R R
R R R
R R R R
R R R R R
>>> clock.updateMinutes()
Clock(0, 0)
>>> clock.lamps()
((0, 0, 0, 0, 0), 'G')
>>> print(clock)
.
. .
. . .
. . . .
. . . . .
>>> clock.updateHours(10).updateMinutes(17)
Clock(10, 17)
>>> clock.lamps()
((1, 2, 0, 2, 5), 'G')
>>> print(clock)
G
G G
. . .
G G . .
G G G G G
>>> Clock(42, 42)
Traceback (most recent call last):
AssertionError: invalid time
Epilogue
Feel free to play around with this interactive triangular clock.