Dummy variabelen
Het lineaire regressiemodel kan ook gebruikt worden voor het vergelijken van twee gemiddelden. In het Borstkanker voorbeeld kunnen we bijvoorbeeld nagaan of er een verschil is in de gemiddelde leeftijd van de patiënten met onaangetaste lymfeknopen en patiënten waarvan de lymfeknopen werden verwijderd.
Hiervoor definiëren we eerst een dummy variabele
\[x_i = \left\{ \begin{array}{ll} 1 & \text{aangetaste lymfeknopen} \\ 0 & \text{onaangetaste lymfeknopen} \end{array}\right.\]De groep met \(x_i=0\) wordt de referentiegroep genoemd. Het regressiemodel blijft ongewijzigd,
\[Y_i = \beta_0 + \beta_1 x_i +\epsilon_i\]met \(\epsilon_i \text{ iid } N(0,\sigma^2)\).
Gezien \(x_i\) slechts twee waarden kan aannemen, is het eenvoudig om het regressiemodel voor beide waarden van \(x_i\) afzonderlijk te bekijken:
\[\begin{array}{lcll} Y_i &=& \beta_0 +\epsilon_i &\text{onaangetaste lymfeknopen} (x_i=0) \\ Y_i &=& \beta_0 + \beta_1 +\epsilon_i &\text{ aangetaste lymfeknopen} (x_i=1) . \end{array}\]Dus
\[\begin{eqnarray*} E\left[Y_i\mid x_i=0\right] &=& \beta_0 \\ E\left[Y_i\mid x_i=1\right] &=& \beta_0 + \beta_1, \end{eqnarray*}\]waaruit direct de interpretatie van \(\beta_1\) volgt:
\[\beta_1 = E\left[Y_i\mid x_i=1\right]-E\left[Y_i\mid x_i=0\right]\]\(\beta_1\) is dus het gemiddelde verschil in leeftijd tussen patiënten met aangetaste lymfeknopen en patiënten met onaangetaste lymfeknopen (referentiegroep).
Met de notatie \(\mu_1= E\left[Y_i\mid x_i=0\right]\) en \(\mu_2= E\left[Y_i\mid x_i=1\right]\) wordt dit
\[\beta_1 = \mu_2-\mu_1.\]Er kan aangetoond worden dat
\[\begin{array}{ccll} \hat\beta_0 &=& \bar{Y}_1&\text{ (steekproefgemiddelde in referentiegroep)} \\ \hat\beta_1 &=& \bar{Y}_2-\bar{Y}_1&\text{(schatter van effectgrootte)} \\ \text{MSE} &=& S_p^2 . \end{array}\]De testen voor \(H_0:\beta_1=0\) vs. \(H_1:\beta_1\neq0\) kunnen gebruikt worden voor het testen van de nulhypothese van de two-sample \(t\)-test, \(H_0:\mu_1=\mu_2\) t.o.v. \(H_1:\mu_1\neq\mu_2\).
brca$node=as.factor(brca$node)
lm3 <- lm(age~node,brca)
t.test(age ~ node, brca, var.equal=TRUE)
##
## Two Sample t-test
##
## data: age by node
## t = -2.7988, df = 30, p-value = 0.008879
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -15.791307 -2.467802
## sample estimates:
## mean in group 0 mean in group 1
## 59.94737 69.07692
summary(lm3)
##
## Call:
## lm(formula = age ~ node, data = brca)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.9474 -5.3269 0.0526 5.3026 18.0526
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 59.947 2.079 28.834 < 2e-16 ***
## node1 9.130 3.262 2.799 0.00888 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.063 on 30 degrees of freedom
## Multiple R-squared: 0.207, Adjusted R-squared: 0.1806
## F-statistic: 7.833 on 1 and 30 DF, p-value: 0.008879
par(mfrow=c(2,2))
plot(lm3)
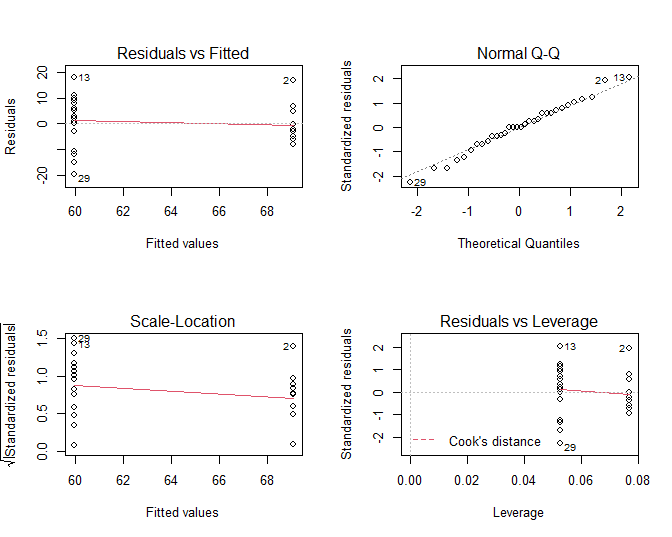
Figuur 39: Diagnostische plot voor het model waarbij leeftijd wordt gemodelleerd a.d.h.v. een dummy variabele voor factor lymfe knoop status.
We zien in de R output dat de output van de t-test en het lineaire model met 1 dummy variabele identieke resultaten geeft voor de test statistiek en de p-waarde. We zien eveneens een heel significante associatie tussen de leeftijd en de lymfe node status (p=0.009). De leeftijd van personen met aangetaste lymfeknopen is gemiddeld 9.1 jaar hoger dan die van patiënten zonder aantasting van de lymfeknopen.
Let op: We kunnen echter niet besluiten dat oudere personen een hoger risico hebben op aantasting van de lymfeknopen ten gevolge van hun leeftijd. Aangezien de studie een observationele studie is, kunnen de groepen patiënten met aangetaste lymfeknopen en niet-aangetaste lymfeknopen nog in andere karateristieken van elkaar verschillen. We kunnen dus enkel besluiten dat er een associatie is tussen de lymfeknoop status en de leeftijd. Het is dus niet noodzakelijkerwijs een causaal verband! Het is immers steeds moeilijk om causale verbanden te trekken op basis van observationele studies gezien confounding kan optreden. We hebben de patiënten immers niet kunnen randomiseren over de twee groepen, de lymfeknoopstatus werd niet geïnduceerd door de onderzoekers maar enkel geobserveerd en we kunnen daarom niet garanderen dat de patiënten enkel verschillen in de lymfeknoopstatus!
Hetzelfde geldt voor het lineair model voor de \(\log_2\)-S100A8-expressie. Aangezien we de ESR1-expressie niet experimenteel vast hebben kunnen leggen, kunnen we niet besluiten dat een hogere ESR1-expressie de S100A8-expressie doet verlagen. We hebben beide genexpressies enkel geobserveerd dus kunnen we alleen besluiten dat ze negatief geassocieerd zijn met elkaar. Om te evalueren of de expressie van een bepaald gen de expressie van ander genen beïnvloedt, gaat men vaak knockout constructen generenen in het labo, dat zijn mutanten die een bepaald gen niet tot expressie kunnen brengen. Wanneer de wild type (normale genotype) en de knockout dan onder identieke condities worden opgegroeid in het lab, weten onderzoekers dat verschillen in genexpressie worden geïnduceerd door de afwezigheid van de expressie van het knockout gen. Experimentele studies zijn immers essentieel om causale verbanden te kunnen trekken.
Veronderstellingen: We moeten echter ook nog de veronderstellingen
van het model voor de leeftijd nagaan! In Figuur
39 zien we geen afwijkingen van normaliteit
in de QQ-plot. Er lijkt echter wel een aanwijzing dat de variantie in
beide groepen verschillend is. De residuen lijken meer gespreid in de
groep met lagere gemiddelde leeftijd (node=0) dan in de groep met een
hogere gemiddelde leeftijd (node=1).
Merk echter ook op dat er een verschil is in het aantal observaties in
beide groepen. Wanneer we een boxplot maken, zoals we ook deden in het
hoofdstuk 5 om gelijkheid van variantie na
te gaan bij het uitvoeren van een t-test, zien we dat het verschil in
interkwartiel afstand (IRQ, boxgrootes) niet zo groot is (Figuur
40). Als we data simuleren die \(iid\)
normaal verdeeld zijn en deze at random opslitsen in twee groepen die
gelijk zijn in grootte als die voor de lymfeknoop status (19 vs 13
patiënten) zien we dat een dergelijk verschil in IQR gerust kan
voorkomen door toeval (Figuur 41). We kunnen
dus besluiten dat aan alle aannames is voldaan voor de statistische
besluitvorming en dat we de R-output van het statistisch model voor de
response age i.f.v de dummy variabele voor de node-status mogen
gebruiken om conclusies te formuleren over de associatie tussen leeftijd
en node status (zie hoger).
brca %>%
ggplot(aes(x = node%>%as.factor, y = age)) +
geom_boxplot() +
xlab("node")
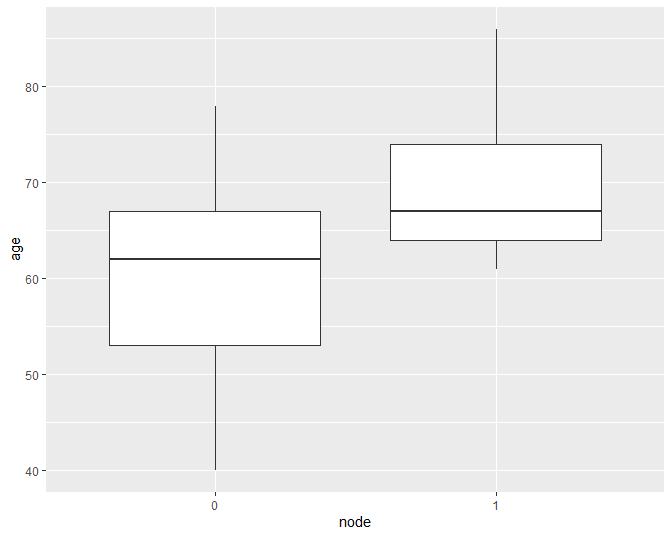
Figuur 40: boxplot van de leeftijd vs lymfeknoop status in de borstkanker dataset.
- Simulate 9 datasets with the same number of observations as the brca dataset from a normal distribution with the same standard deviation as in the original data. Store the data of all simulations in a data frame
- Plot the simulated data using the
ggplotfunction - Add a boxplot layer
- Use facet_wrap to make a separate plot for simulated dataset
- Change label of y axis
set.seed(354)
sim_df <- data.frame(
node = rep(brca$node, 9),
iid = rnorm(9 * nrow(brca), sd = sigma(lm3)),
sim = rep(1:9, each = 32)
)
sim_df %>%
ggplot(aes(x = node, y=iid)) +
geom_boxplot() +
facet_wrap(.~sim) +
ylab(paste0("iid N(0,",round(sigma(lm3)^2,2),")"))

Figuur 41: Simulatie van normaal verdeelde gegevens met gelijk gemiddelde en variantie. Zoals in de borstkanker dataset zijn er 19 observaties in ene groep en 13 observaties in de andere groep. We zien dat er door puur toeval een behoorlijk verschil kan optreden in de IQR tussen beide groepen in de steekproef.
Zoals we illustreerden is het steeds nuttig om simulaties te gebruiken om in te leren schatten wanneer de diagnostische plots duiden op een afwijking van de voorwaarden.